Докажите что векторы перпендикулярны

Ортогональность векторов. Перпендикулярность векторов.

Вектора a и b называются ортогональными, если угол между ними равен 90°. (рис. 1).

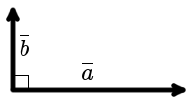рис. 1

Примеры задач на ортогональность векторов

Примеры плоских задач на ортогональность векторов

Найдем скалярное произведение этих векторов:

Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.

Найдем скалярное произведение этих векторов:

Ответ: так как скалярное произведение не равно нулю, то вектора a и b не ортогональны.

Найдем скалярное произведение этих векторов:

Примеры пространственных задач на ортогональность векторов

Так в случае пространственной задачи для векторов a = < a_x ; a_y ; a_z > и b = < b_x ; b_y ; b_z >, условие ортогональности запишется следующим образом:

Найдем скалярное произведение этих векторов:

Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.

Найдем скалярное произведение этих векторов:

Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.

Найдем скалярное произведение этих векторов:

Ответ: вектора a и b будут ортогональны при n = 2.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Источник

Практическая работа по математике на тему «Коллинеарность и перпендикулярность векторов»

Определение коллинеарности и перпендикулярности векторов

Цель работы: при выполнении работы вы научитесь определять коллинеарность и перпендикулярность векторов, решать простейшие задачи с использованием определений и свойств.

При выполнении практической работы следует придерживаться следующих правил:

практическую работу следует выполнять в отдельной тетради для практических и домашних работ, чернилами любого цвета кроме красного, оставляя поля для рецензий;

решение задач должно располагаться в порядке возрастания их номеров, сохраняя нумерацию заданий;

перед решением каждой задачи нужно записать полностью её условие;

решение задач следует излагать подробно и аккуратно, объясняя и мотивируя все действия по ходу решения и выполняя необходимые чертежи.

Вектор – «направленный» отрезок. Векторы в прямоугольной системе координат задаются с помощью его координат.

Длиной ненулевого вектора называется длина отрезка АВ. Обозначается так: или ( ).

Вектор всегда можно получить из двух точек М(х ₁ ; у ₁ ; z ₁ ) и N (х ₂ ; у ₂ ; z ₂ ).

Для того чтобы проверить коллинеарность векторов, заданных своими координатами и надо проверить выполнение равенств:

Угол между двумя векторами можно всегда получить, отложив векторы от общей точки.

Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними.

Для того чтобы проверить перпендикулярность векторов, заданных своими координатами и надо вычислить их скалярное произведение и далее проверить утверждение: скалярное произведение равно нулю тогда и только тогда, когда векторы перпендикулярны.

Задание 1. Постройте векторы и коллинеарные сонаправленные векторы.

Задание 3. Даны точки А(-2; 3; 1), В(-2; 1; 2) и С(0; 3; 4). Проверьте перпендикулярность векторов АВ и АС.

Задание 5. В тетраэдре ДАВС ДА= 5 см, АВ = 4 см, АС = 3 см,

Задания выполняются в аудитории во время практических занятий. После выполнения заданий предусматривается защита работы (в полном объеме или частично).

Оценка 5 – при выполнении 5 заданий за 45 минут;

Оценка 4 – при выполнении 4 заданий за 45 минут;

Оценка 3 – при выполнении 3-х заданий;

Оценка 2 – при выполнении менее 3-х заданий.

Защита работы предполагает демонстрация решения заданий на классной доске, ответы на вопросы. Если работу выполняет группа, то все ее участники должны владеть всей информацией и способом решения.

Задание 1. Постройте векторы и коллинеарные противоположно направленные векторы.

Задание 5. В тетраэдре ДАВС ДА= 5 см, АВ = 4 см, АС = 3 см,

Задания выполняются в аудитории во время практических занятий. После выполнения заданий предусматривается защита работы (в полном объеме или частично).

Оценка 5 – при выполнении 5 заданий за 45 минут;

Оценка 4 – при выполнении 4 заданий за 45 минут;

Оценка 3 – при выполнении 3-х заданий;

Оценка 2 – при выполнении менее 3-х заданий.

Защита работы предполагает демонстрация решения заданий на классной доске, ответы на вопросы. Если работу выполняет группа, то все ее участники должны владеть всей информацией и способом решения.

Задание 5. В тетраэдре ДАВС ДА= 5 см, АВ = 4 см, АС = 3 см,

Задания выполняются в аудитории во время практических занятий. После выполнения заданий предусматривается защита работы (в полном объеме или частично).

Оценка 5 – при выполнении 5 заданий за 45 минут;

Оценка 4 – при выполнении 4 заданий за 45 минут;

Оценка 3 – при выполнении 3-х заданий;

Оценка 2 – при выполнении менее 3-х заданий.

Защита работы предполагает демонстрация решения заданий на классной доске, ответы на вопросы. Если работу выполняет группа, то все ее участники должны владеть всей информацией и способом решения.

Задание 5. В тетраэдре ДАВС ДА= 5 см, АВ = 4 см, АС = 3 см,

Задания выполняются в аудитории во время практических занятий. После выполнения заданий предусматривается защита работы (в полном объеме или частично).

Оценка 5 – при выполнении 5 заданий за 45 минут;

Оценка 4 – при выполнении 4 заданий за 45 минут;

Оценка 3 – при выполнении 3-х заданий;

Оценка 2 – при выполнении менее 3-х заданий.

Защита работы предполагает демонстрация решения заданий на классной доске, ответы на вопросы. Если работу выполняет группа, то все ее участники должны владеть всей информацией и способом решения.

Задание 5. В тетраэдре ДАВС ДА= 5 см, АВ = 4 см, АС = 3 см,

Задания выполняются в аудитории во время практических занятий. После выполнения заданий предусматривается защита работы (в полном объеме или частично).

Оценка 5 – при выполнении 5 заданий за 45 минут;

Оценка 4 – при выполнении 4 заданий за 45 минут;

Оценка 3 – при выполнении 3-х заданий;

Оценка 2 – при выполнении менее 3-х заданий.

Защита работы предполагает демонстрация решения заданий на классной доске, ответы на вопросы. Если работу выполняет группа, то все ее участники должны владеть всей информацией и способом решения.

Задание 3. Даны точки А(0; 1; 2), В(; 2; 1), С(; 2; 1) и Д(0; 2; 1). Докажите, что АВСД – квадрат.

Задание 5. В тетраэдре ДАВС ДА= 5 см, АВ = 4 см, АС = 3 см,

Задания выполняются в аудитории во время практических занятий. После выполнения заданий предусматривается защита работы (в полном объеме или частично).

Оценка 5 – при выполнении 5 заданий за 45 минут;

Оценка 4 – при выполнении 4 заданий за 45 минут;

Оценка 3 – при выполнении 3-х заданий;

Оценка 2 – при выполнении менее 3-х заданий.

Защита работы предполагает демонстрация решения заданий на классной доске, ответы на вопросы. Если работу выполняет группа, то все ее участники должны владеть всей информацией и способом решения.

Задание 3. Даны точки А(0; 1; 2), В(; 2; 1), С(; 2; 1) и Д(0; 2; 1). Докажите, что АВСД – квадрат.

Задание 5. В тетраэдре ДАВС ДА= 5 см, АВ = 4 см, АС = 3 см,

Задания выполняются в аудитории во время практических занятий. После выполнения заданий предусматривается защита работы (в полном объеме или частично).

Оценка 5 – при выполнении 5 заданий за 45 минут;

Оценка 4 – при выполнении 4 заданий за 45 минут;

Оценка 3 – при выполнении 3-х заданий;

Оценка 2 – при выполнении менее 3-х заданий.

Защита работы предполагает демонстрация решения заданий на классной доске, ответы на вопросы. Если работу выполняет группа, то все ее участники должны владеть всей информацией и способом решения.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-1544282

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

ДНР полностью перешла на стандарты и программы России в образовании

Время чтения: 1 минута

В России отцы охотнее дают деньги детям на карманные расходы, чем матери

Время чтения: 2 минуты

В Ленобласти педагоги призеров и победителей олимпиады получат денежные поощрения

Время чтения: 1 минута

Минпросвещения разработает внеучебные курсы для школьников

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник