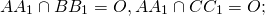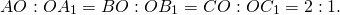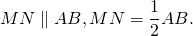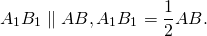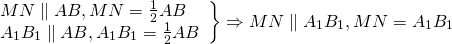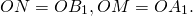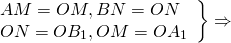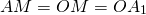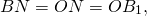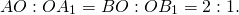Докажите методом координат что медианы треугольника пересекаются в одной точке
Применение метода координат к решению задач элементарной геометрии.
ПРИМЕР 2.11
Доказать, что медианы треугольника пересекаются в одной точке и делятся в ней в отношении 2 : 1, начиная от вершин.
Пусть АМ, ВN, СР медианы треугольника АВС (Рис.2.5). Рассмотрим систему координат (А, 





| А |
| В |
| С |
| М |
| Р |
| N |
Обозначим через Х, У, Z точки, которые делят соответственно медианы АМ, ВN, СР в отношении 2 : 1, начиная от вершин А, В, С., тогда простые отношения (АМ,Х) = (ВN,У) = (СР,Z) = 2.
Теперь используя формулы деления отрезка в данном отношении
х = 







ПРИМЕР 2.12
Доказать, что сумма квадратов диагоналей трапеции равна сумме квадратов ее боковых сторон, сложенной с удвоенным произведением оснований трапеции.
Пусть АВСD- произвольная трапеция с основаниями АВ и СD (Рис.2.6). Рассмотрим прямоугольную декартову систему координат (А, i, j ), где
i↑↑ 
| А(0,0) |
| В(а,0) |
| D (d,m) |
| C(c,m) |
| i |
| j |
АС 2 + ВD 2 = с 2 + m 2 + ( d – а) 2 + m 2 = а 2 + с 2 + d 2 + 2m 2 – 2ad.
АD 2 + ВС 2 + 2АВ DС = d 2 + m 2 + (с – а) 2 + m 2 + 2а (с – d) =
а 2 + с 2 + d 2 + 2m 2 – 2ad.
Из этого следует, что АС 2 + ВD 2 = АD 2 + ВС 2 + 2АВ DС. ▄
2.87. Доказать, что средняя линия треугольника параллельна основанию и равна его половине.
2.88. Доказать, что средняя линия трапеции параллельна основаниям и равна их полусумме.
2.89. Доказать, что отрезок, соединяющий середины диагоналей трапеции, параллелен основаниям и равен их полуразности.
2.90. Доказать, что медиана равнобедренного треугольника проведенная к основанию является высотой и биссектрисой.
2.91. Доказать, что если диагонали трапеции равны, то трапеция равнобедренная.
2.92. Доказать, что в параллелограмме сумме квадратов диагоналей равна сумме квадратов всех сторон.
2.93. Через вершину А треугольника АВС и середину Е медианы СD проведена прямая, пересекающая сторону ВС в точке F. а) Доказать, что СF : FВ = 1 : 2.
б) Найти в каком отношении точка Е делит отрезок АF.
2 94. Точка пересечения диагоналей четырехугольника совпадает с точкой пересечения его средних линий. Доказать, что данный четырехугольник является параллелограммом.
2 95. Даны параллелограмм АВСD и точка М. Точка М1 симметрична точке М относительно вершины А. Точка М2 симметрична точке М1 относительно вершины В. Точка М3 симметрична точке М2 относительно вершины С. Точка М4 симметрична точке М3 относительно вершины D. Доказать, что точка М4 совпадает с точкой М.
2.96. Даны две окружности ω1(О1,r1) и ω2(О2,r2). Доказать, что сумма квадратов расстояний от концов любого диаметра первой окружности до концов любого диаметра второй окружности постоянна.
ОТВЕТЫ И УКАЗАНИЯ К ГЛАВЕ 2
2.3. 

б) С(4 



2.6. А(0,0), В(1,0), С( 







2.11. а) 5; б) 
2.12. а) 
2.13. (14,0), (0, 
2.15. а) равносторонний; б) равнобедренный; в) прямоугольный.
2.17. Существует два треугольника АВС1 и АВС2.
2.18. (2,10). Указание. Так как ось ОХ касается окружности в точке В, то
х = 2, далее воспользоваться тем, что АМ = ВМ.
2.20. а) 


2.22. А( 



2.26. 
2.28.С( 
2.29. ( 

ВD : DС = АВ :АС и значит (ВС, D) = АВ : АС.
2.30. 
2.32. 




2.34. а) и б) положительная ориентация, 3) отрицательная ориентация.
2.37. а), г) – левый базис, б), в) – правый базис.
2.38. Ι│ΙΙ = 1, ΙΙ – правый базис.
2.41. а) 

б) х = х ′+ 2у ′+ 1, у = 4х′+ 3у ′ + 1.
2.50. а) х = 




б) х = 



2.51. ( 

2.52. Все точки прямой х + у – 2 = 0.
б) А: ρ = 0, φ не определен, В(1,0), С(1, 
б) А: : ρ = 0, φ не определен, В(3, 


б) А: ρ = 0, φ не определен, В(2, 


2.62. а)Окружность с центром О и радиусом 1;
б) Окружность с центром О и радиусом 
в) Открытый луч с началом О, образующий с полярной осью
угол 
б) М(6, 



2.64. а) 
2.66. а) Прямая, перпендикулярная полярной оси и проходящая через
точку с полярными координатами (2,0);
б) Окружность радиуса 5 с центром (5, 
в) Прямая, параллельная полярной оси и проходящая через
точку (1, 
г) Две прямые, проходящие через начало полярной системы
координат и образующие с полярной осью углы 

2.69. а) φ = arctg 
в) ρ 2 (1 + Cos 2 φ) = 5;
2.70. (х + 1) 2 + (у – 3) 2 = 16.
г) М(-1, 

д) Окружность с центром (1, 0) и радиусом r = 1;
ж) Окружность с центром (2,1) и радиусом r = 2;
Остальные уравнения не определяют окружность.
2.74. Точки А, С, D лежат вне окружности, точка В на окружности.
2.75. а) Точки находятся вне или на окружности с центром (1,3) и
б) Точки расположены между двумя концентрическими
окружностями и на самих окружностях, радиусы которых
в) Точки принадлежат общей части двух кругов и границе кругов,
центры которых в точках (1,2) и (4,6) и радиусы равны 5 и 3.
2.78. (х – 3) 2 + (у + 4) 2 = 25.
2.79. (х – 1) 2 + (у + 3) 2 = 68.
2.80. (х – 3) 2 + (у – 2) 2 = 26 и (х + 3) 2 + (у – 6) 2 = 26.
2.81. (х – 2) 2 + (у – 3) 2 = 1. Указание. Так как центр М окружности лежит на прямой
3х –у – 3 = 0, то М имеет координаты М(х, 3х – 3).
2.82. (х + 3) 2 + у 2 = 8.
2.84. х 2 + (у – 3) 2 = 9.
2.85. Окружность с центром в точке пересечения данных прямых и радиусом 4. Указание. Рассмотреть прямоугольную декартову систему координат, оси которой совпадают с данными прямыми.
2.86. Прямая с уравнением 4х – 9 = 0.
2.87. Указание. Пусть МN средняя линия треугольника АВС. Рассмотреть систему координат (А, 

2.88. Указание. Пусть АВСD – трапеция с основаниями АВ и СD. Рассмотреть систему координат (А, 

2.89. Указание. Пусть АВСД – трапеция с основаниями АВ и СД. Рассмотреть систему координат (А, 

2.90. Указание. Пусть АD – медиана треугольника АВС (АВ = АС). Рассмотреть систему координат (D, i, j ), где i↑↑ 

2.91.Указание. Пусть АВСD – трапеция с основаниями АВ и СD. Рассмотреть систему координат (О, i, j ), где i↑↑ 
2.92. Указание. Пусть АВСD –параллелограмм. Рассмотреть систему координат
(А, i, j ), где i↑↑ 
2 93.(АF,Е) = 3. Указание. Рассмотреть систему координат (А, 

2.95.Указание. Рассмотреть систему координат (А, 

2.96. Указание. Рассмотреть систему координат (О1, i, j ), где i↑↑ 
2.97.Указание. Рассмотреть систему координат (А, 

(АВ,С1) = α, (ВС, А1) = β, (СА, В1) = γ, найти координаты точек А1, В1, С1 и использовать то, что эти точки лежать на одной прямой тогда и только тогда, когда векторы 

ГЛАВА 3.
ПРЯМАЯ ЛИНИЯ НА ПЛОСКОСТИ

Свойство медиан треугольника
Свойство медиан треугольника может быть доказано многими способами. Доказательство, опирающееся на свойства параллелограмма и средней линии треугольника, может быть проведено сразу же после изучения соответствующих тем, что позволяет начать использовать свойство медиан треугольника уже с начала 8 класса.
(Свойство медиан треугольника)
Медианы треугольника пересекаются и в точке пересечения делятся в отношении 2:1, считая от вершины.


2) Соединим точки M, N, A1 и B1 отрезками.
3) Так как AA1 и BB1 — медианы треугольника ABC, точка A1- середина отрезка BC, B1 — середина AC.
Следовательно, A1B1 — средняя линия треугольника ABC и
Значит, четырёхугольник MNA1B1 — параллелограмм (по признаку).
По свойству диагоналей параллелограмма
из чего следует, что
5) Доказательство того факта, что все медианы треугольника пересекаются в одной точке, будем вести методом от противного.
Предположим, что третья медиана CC1 треугольника ABC пересекает медианы AA1 и BB1 в некоторой точке, отличной от точки O.
Тогда на каждой медиане есть две различные точки, делящие её в отношении 2:1, считая от вершины. Пришли к противоречию.
Таким образом, все три медианы треугольника пересекаются в одной точке и точка пересечения медиан делит каждую из их в отношении 2:1, считая от вершины:
7 Comments
Промогите пожалуйста:
В прямоугольном треугольнике из вершины прямого угла до гипотенузы провели медиану длинной 50см и перпендикуляр 48см. Вычислить периметр.
Медиана, проведённая к гипотенузе, равна её половине. Следовательно, гипотенуза 100 см. Пусть катеты равны x см и y см. По теореме Пифагора x²+y²=100². Площадь треугольника равна половине произведения стороны на высоту, проведённую к этой стороне S=0,5∙100∙48 см², либо половине произведения катетов S=0,5∙x∙y. Отсюда xy=4800.
Решаем систему уравнений: x²+y²=100²; xy=4800. Решения (60;80) (80;60). То есть катеты 60 см и 80 см. Периметр P=60+80+100=240 см.
(Не обязательно доводить решение системы до конца. Достаточно найти x+y. Для этого к 1-му уравнению прибавим удвоенное 2-е, получим
x²+2xy+y²=19600; x+y=140).
Прошу помощи в решении задачи: на стороне ромба построен равносторонний треугольник. Отрезок, соединяющий точку пересечения диагоналей ромба с серединой стороны треугольника, составляет с ней угол 70 градусов. Найти острый угол ромба.
Во-первых, большое спасибо за решение, даже не ожидала ответа, но, по счастью, ошиблась! Но я к этому времени уже решила так:провела ВМ, которая в равностороннем треугольнике является также высотой.
Рассмотрим четырехугольник ОВМС: угол ВОС =углу ВМС=90 градусов (диагонали ромба взаимно перпендикулярны),отсюда, ВМ параллельна ОС, тогда угол МОС=20 градусам. Рассм. треугольник ОМС: угол МСО= 180-20-70=90 градусов, и одновременно= 60+x, т.о., угол х=30 градусам, и искомый острый угол ромба=60 градусам. Мы получили разные ответы, в чем может быть дело (окружности мы еще не проходили).
Наталия углы BOC и BMC не накрест лежащие и не внутренние односторонние, поэтому BM не параллельна OC. Но вариант решения без окружности возможен, добавила второй способ.