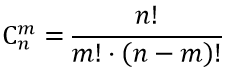Два равносильных шахматиста играют в шахматы что вероятнее

Решение задач про шахматные партии

Чаще всего в задаче про партии следует вычислить две вероятности и сравнить:

Два равносильных шахматиста играют в шахматы. Что вероятнее: выиграть 2 партии из 4 или 3 партии из 6 (ничьи во внимание не принимаются).

Видеоурок и шаблон Excel

Посмотрите наш ролик о решении задач об играх и партиях: как использовать Excel для решения типовых задач с игроками и партиями (как для малого, так и для большого числа партий).

Расчетный файл Эксель из видео можно бесплатно скачать и использовать для решения своих задач.

Примеры решений задач о шахматных партиях

Рассмотрим несколько типовых примеров.

Пример 1. Два равносильных шахматиста играют в шахматы. Что вероятнее выиграть 2 партии из 4 или 3 партии из 6 (ничьи во внимание не принимаются).

Пример 2. Играет два равных по силе игрока, какая вероятность выше: выиграть одну партию из трех, или три из пяти.

Пример 3. Играют равносильные противники. Что вероятнее: выиграть не менее трех партий из четырех или не менее шести из восьми? (Ничьи не учитываются)

В отличие от предыдущих задач, здесь нужно найти вероятность того, что число выигрышных партий будет находится в некотором интервале (а не равно в точности какому-то числу). Но формула используется по-прежнему таже самая.

Найдем вероятность выиграть не менее трех партий из четырех, то есть вероятность выиграть или три партии, или четыре партии. Данные вероятности равны по формуле (1):

Аналогично находим вторую вероятность выиграть не менее 6 партий из 8 (то есть выиграть или 6, или 7, или 8 партий). В этот раз все вычисления запишем сразу в одну формулу:

Итак, вероятнее выиграть не менее 3 партий из 4 (так как 0,3125 больше чем 0,145).

Пример 4. Какова вероятность, что игрок, который слабее своего оппонента в два раза выиграет две партии из трех

Для полноты изложения приведу решение этой задачи, с первого взгляда она похожа на предыдущие (и так и есть, конечно), но есть некоторое отличие. А именно, противники тут не равносильные, а один слабее другого. С точки зрения формализации задачи, это будет означать, что вероятность выигрыша для игрока равна не 0,5, а другому числу. Какому?

Источник

Формула Бернулли

Если в n испытаниях событие А случается (происходит) k раз и не случается (не происходит) (n-k) раз, то данную вероятность Р_n(k) можно найти по формуле Бернулли:

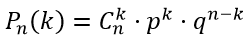
где
p — вероятность успеха испытания (опыта);
q=1-p — вероятность неудачи испытания (вероятность противоположного события);
$C_n^k$ — число сочетаний, вычисляется по формуле комбинаторики — сочетание без повторения

Пример 1
Монету бросают шесть раз. Найти вероятность того, что герб выпадет не менее двух раз.

Пример 2

Каждый день акции компании X поднимаются в цене или падают в цене на один пункт с вероятностями 0,75 и 0,25. Найти вероятность того, что акции после 6 дней вернутся к своей первоначальной цене, то есть чтобы акции за это время 3 раза поднялись в цене и три раза опустились в цене. При этом изменения цены акции вверх и вниз – независимые события.

Решение

Пример 4
Два равносильных противника играют в шахматы.
Что вероятнее:
а) выиграть одну партию из двух или две партии из четырех?
б) выиграть не менее двух партий из четырех или не менее трех партий из пяти? Ничьи во внимание не принимаются.
Решение
Вероятность выигрыша шахматиста равна р=1/2, а вероятность проигрыша шахматиста
q=1-p=0.5
а) По формуле Бернулли найдём вероятность P₂(1) «выиграть одну партию из двух» и вероятность P₄(2) «выиграть две партии из четырех»

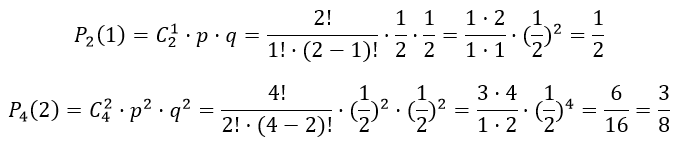
Имеем P₂(1)>Р₄(2) следовательно, вероятнее в шахматы выиграть одну партию из двух, чем две партии из четырех.
б) Сначала рассмотрим событие A — «выиграть не менее двух партий из четырех», которое соответствует сумме независимых событий Р₄(2), Р₄(3), Р₄(3), то есть «выиграть две или три или четыре партии из четырех»

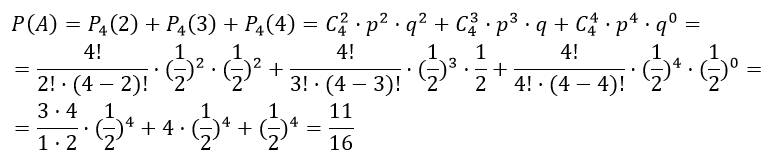
Теперь рассмотрим событие В — «выигрыш не менее трех партий из пяти», которое соответствует сумме независимых событий Р₅(3), Р₅(4), Р₅(5), то есть «выиграть три или четыре или пять партий из трех»

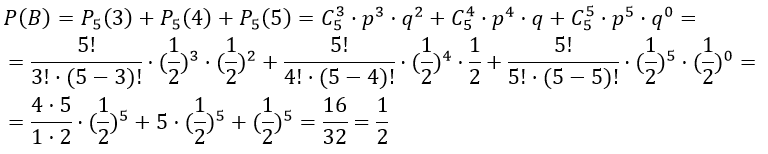
Здесь Р(А)>P(B), следовательно, вероятнее выиграть не менее двух партий из четырех, чем не менее трех партий из пяти.

Источник

Два равносильных шахматиста играют в шахматы. Что вероятнее выиграть: две партии из четырёх или три из шести?

Готовое решение: Заказ №8392

Тип работы: Задача

Статус: Выполнен (Зачтена преподавателем ВУЗа)

Предмет: Теория вероятности

Дата выполнения: 30.09.2020

Цена: 208 руб.

Описание и исходные данные задания, 50% решения + фотография:

В задачах 601-620 применить формулу Бернулли, локальную и интегральную теоремы Лапласа.

Условие 2

Два равносильных шахматиста играют в шахматы. Что вероятнее: выиграть две партии из четырёх или три партии из шести (ничьи во внимание не принимаются)?

Решение.

Поскольку противники равносильны, то вероятность победы p и вероятность поражения q одинаковы и равны:

(ничьи в расчёт не принимаются).

Тогда вероятность того, что в n партиях будет ровно m побед, будет вычисляться по формуле Бернулли:

где – число сочетаний.

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник

Два равносильных противника играют в шахматы. Что вероятнее: выиграть не менее двух партий из четырёх или не менее трёх партий из пяти? Ничьи во внимание не принимаются.

Готовое решение: Заказ №8392

Тип работы: Задача

Статус: Выполнен (Зачтена преподавателем ВУЗа)

Предмет: Теория вероятности

Дата выполнения: 30.09.2020

Цена: 208 руб.

Описание и исходные данные задания, 50% решения + фотография:

Два равносильных противника играют в шахматы. Что вероятнее: выиграть не менее двух партий из четырёх или не менее трёх партий из пяти? Ничьи во внимание не принимаются.

Решение.

Поскольку противники равносильные и ничьи в расчёт не принимаются, то вероятность победы p и вероятность поражения q одинаковы и равны:

где – число сочетаний.

Найдём вероятность выиграть не менее двух партий из четырёх:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник

Два равносильных противника играют в шахматы

Пусть проводится n независимых испытаний, в каждом из которых событие А происходит с вероятностью p. При этом вероятность противоположного события равна

В теории вероятностей особый интерес представляет случай, когда в n испытаниях событие А встречается k раз, тем самым не встречается (n-k) раз.

Монету подбрасывают шесть раз. Какова вероятность того, что герб выпадет только два раза.

Для вычисления искомой вероятности применим формулу Бернулли. Число испытаний n=6. а число благоприятствующих исходов k=2. Вероятность события (выпадения герба)

Два равносильных противника играют в шахматы. Что вероятнее:

а) выиграть одну партию из двух или две партии из четырех?

б) выиграть не менее двух партий из четырех или не менее трех партий из пяти? Ничьи во внимание не принимаются.

Так как играют равносильные шахматисты, то вероятность выигрыша р=1/2. вероятность проигрыша
q=1-p=0.5. Во всех партиях вероятность выигрыша постоянна и безразлично, в какой последовательности произойдут эти выигрыши, поэтому применима формула Бернулли:

Так как P 2 (1) > Р 4 (2). то более вероятен выигрыш одной партии из двух, чем двух партий из четырех.

б) Пусть событие А — «выиграть не менее двух партий из четырех». Данное событие соответствует следующим независимым событиям:

• «выиграть две партии из четырех», вероятность этого события вычисляется как Р 4 (2) ;

• «выиграть три партии из четырех», вероятность этого события вычисляется как Р 4 (3) ;

Пусть событие В — «выигрыш не менее трех партий из пяти». Данное событие соответствует следующим независимым событиям:

• «выиграть три партии из пяти», вероятность этого события вычисляется как Р 5 (3) ;

• «выиграть четыре партии из пяти», вероятность этого события вычисляется как Р 5 (4) ;

Так как Р(А) > P(B). то выигрыш не менее двух партий из четырех более вероятен, чем выигрыш не менее трех партий из пяти.

Похожие игры:

Играть в шахматы бесплатно онлайн с живыми игроками (людьми) 1. Недавно захотел в шахматы сиграть. Вот нашёл неплохую мини-игру, где полностью реализована игра шахматы. К тому же здесь играют жив.

Игра в шахматы с компьютером Для игры в бесплатные шахматы с компьютером в Вашем броузере IE или Mozilla Firefox должна быть включена поддержка JavaScript. Для выполнения хода Вам необходимо сдел.

Игра в шахматы с компьютером Для игры в бесплатные шахматы с компьютером в Вашем броузере IE или Mozilla Firefox должна быть включена поддержка JavaScript. Для выполнения хода Вам необходимо сдел.

Играть в шахматы бесплатно онлайн с живыми игроками (людьми) 1. Недавно захотел в шахматы сиграть. Вот нашёл неплохую мини-игру, где полностью реализована игра шахматы. К тому же здесь играют жив.

Источник