Если работа выполнена на 100 то обычно говорят что выполнена
Задачи на работу и производительность
На это уроке мы рассмотрим разные способы решения задач на работу, чтобы сэкономит время на экзамене!
Мы разберем более 11 примеров (и этого будет достаточно, чтобы решить любую задачу на работу на ЕГЭ)
Let’s do it! (Сделаем это!)
Задачи на работу — коротко о главном
Производительность – это объем работы, выполняемый за единицу времени: \( \displaystyle P=\frac
\)
При совместной работе производительности складываются.
Основная формула задач на работу
Ты уже освоил тему «Задачи на движение»? Задачи на работу – это то же самое.
Основная формула здесь выглядит так:
Производительность – это объем работы, выполняемый за единицу времени (например, за час или за день).
По-другому, скорость выполнения работы. Вася решает \( \displaystyle 5\) задач в час. Это и есть производительность.
Как у тебя дела с физикой? В физике эта величина называется мощностью.
Как и в задачах на движение, нам нужно не зазубрить эти формула, а уметь выражать все эти три величины друг через друга:
| \( \displaystyle P=\frac | \( \displaystyle t=\frac \) | \( \displaystyle A=P\cdot t\) |
Пример:
Заказ на \( \displaystyle 112\) деталей первый рабочий выполняет на \( \displaystyle 2\) часа дольше, чем второй. Сколько деталей за час делает первый рабочий, если известно, что второй за час делает на одну деталь больше, чем первый?
Решение:
Пусть производительность первого равна \( \displaystyle x\) (ее нам и нужно найти). Тогда второго — \( \displaystyle (x+1)\). Если первый сделал заказ за время \( \displaystyle t\), тогда второй – за время \( \displaystyle t-2\). Работа равна \( \displaystyle 112\).
1-й способ решения — с помощью таблицы
| Работа \( \displaystyle A\) | Производительность \( \displaystyle P\) | Время \( \displaystyle t\) | \( \displaystyle 112\) | \( \displaystyle x\) | \( \displaystyle t\)\( \displaystyle t-2\) |
| II рабочий | \( \displaystyle 112\) | \( \displaystyle x+1\) |
Для каждой строки можем написать формулу:
Почему я выразил именно время?
У нас здесь система уравнений. А что происходит в системе, если выразить одну неизвестную через другую?
Мы таким образом можем от нее избавиться! Именно это я и собираюсь сделать!
Время нам известно? Нет. Его нам нужно найти? Нет.
Поэтому от неизвестного \( \displaystyle t\) надо избавиться!
Для этого теперь достаточно просто приравнять полученные выражения для \( \displaystyle t\):
Из этих двух ответов, естественно, выбираем положительный: \( \displaystyle x=7\).
2-й способ решения — без таблицы
Как обойтись без составления таблицы?
Сразу составить уравнение.
Для этого определим, какая величина нам не нужна в уравнении, чтобы затем приравнять.
Производительность? Ее и надо найти. Работа? Она нам дана по условию, поэтому глупо от нее избавляться. Остается время: оно нам и неизвестно, и не нужно.
Слева от знака равно будем писать формулу времени для первого рабочего, а справа – для второго.
Напомню, что первый работал на \( \displaystyle 2\) часа дольше, поэтому к времени второго надо будет прибавить \( \displaystyle 2\):
То же самое уравнение, что и в первом способе, только без таблицы и системы уравнений.
А теперь вспомним, что я говорил в сааамом начале: задачи на работу и на движение – это то же самое. Спорное заявление, да? Ну, давай проверим, есть ли аналогия.
Во-первых, сравним формулы:
| Движение | Работа |
| \( \displaystyle v=\frac | \( \displaystyle P=\frac |
| Скорость движения | Скорость выполнения работы, т.е. производительность |
| Пройденный путь | Выполненная работа |
| Потраченное на движение время | Потраченное на работу время |
Теперь рассмотрим задачу:
Пример №1
Расстояние \( \displaystyle 112\) км первый велосипедист проезжает на \( \displaystyle 2\) часа дольше, чем второй.
Сколько км в час проезжает первый велосипедист, если известно, что второй за час проезжает на один километр больше, чем первый?
Ничего не напоминает? Да я же просто заменил слова: «Заказ» на «расстояние», «деталь» на «километр», «рабочий» на «велосипедист», «выполняет» на «проезжает». Суть осталась той же. Даже решение будет точно таким же (разберу здесь только II способ – без таблицы).
Пусть скорость первого \( \displaystyle x\), тогда второго \( \displaystyle x+1\). Сколько времени едет первый? \( \displaystyle \frac<112>
То же самое уравнение! Вот и получается, что работа и движение – одно и то же.
Как решать задачи на совместную работу
Задачи на совместную работу отличаются от обычных, представленных выше, тем, что в них работа выполняется одновременно (совместно) несколькими рабочими (трубами и т.д.).
Пример №2
Первая труба заполняет бассейн за \( \displaystyle 6\) часов, а вторая – за \( \displaystyle 4\).
За какое время они заполнят бассейн, работая вместе?
Решение
Во-первых, давай придумаем аналогию с движением.
Бассейн – это путь. Допустим, из \( \displaystyle A\) в \( \displaystyle B\). Итак, первый автомобиль проезжает путь \( \displaystyle AB\) за \( \displaystyle 6\) часов, второй – за \( \displaystyle 4\).
А теперь как сформулировать вопрос? За какое время они проедут весь путь, двигаясь вместе? Бред.
Если двигаться параллельно, то каждый проходит весь путь самостоятельно. А в какой ситуации нам важно, какой путь автомобили проходят в сумме? Все гениальное просто: если они движутся навстречу друг другу!
Тогда что нас просят найти? Время, через которое они встретятся.
Поразмысли немного над этой аналогией. Все понял? Тогда идем дальше.
Какова «скорость» (а по-настоящему, производительность) первого? Путь (работа) деленный на время: \( \displaystyle <
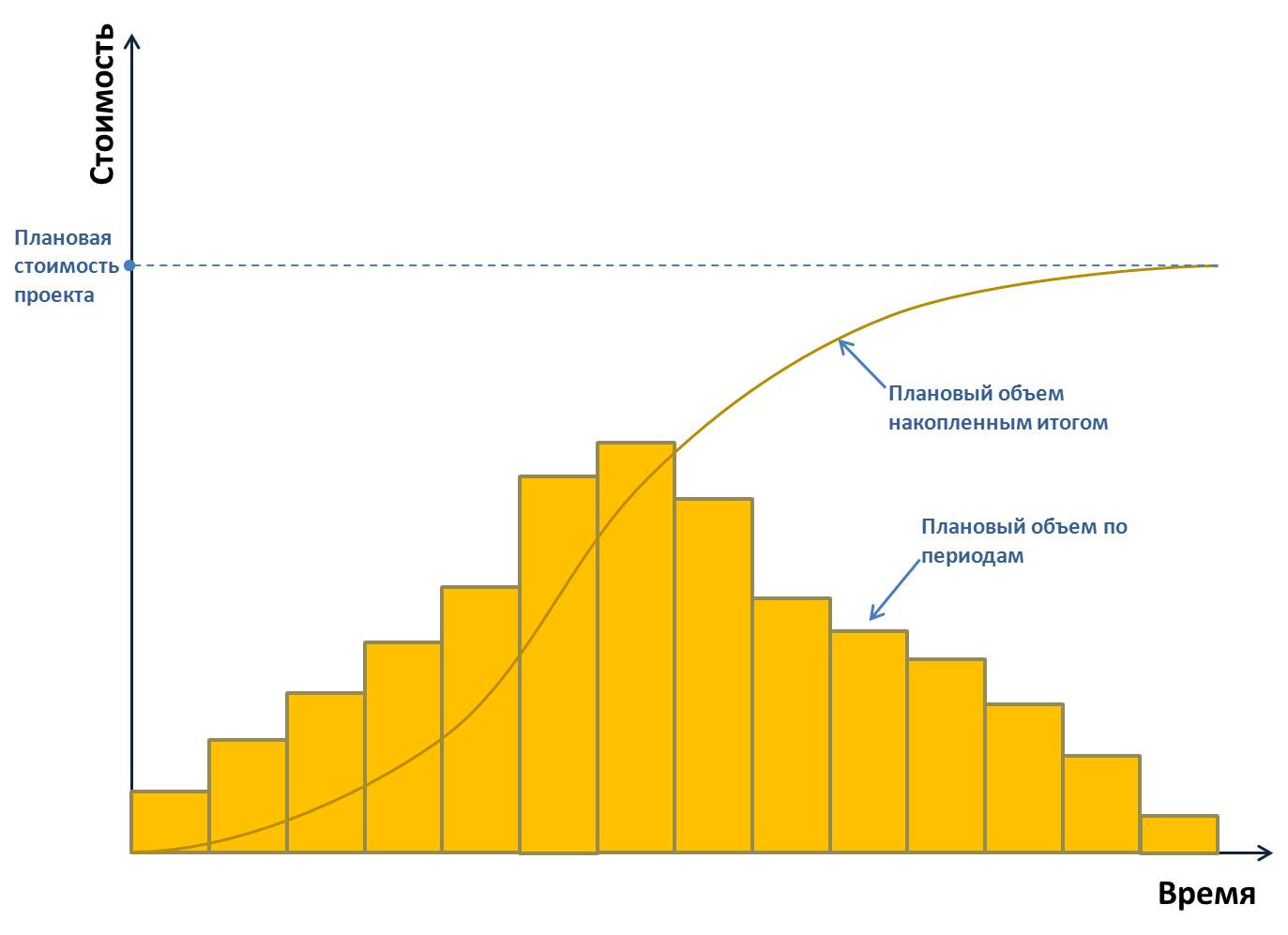
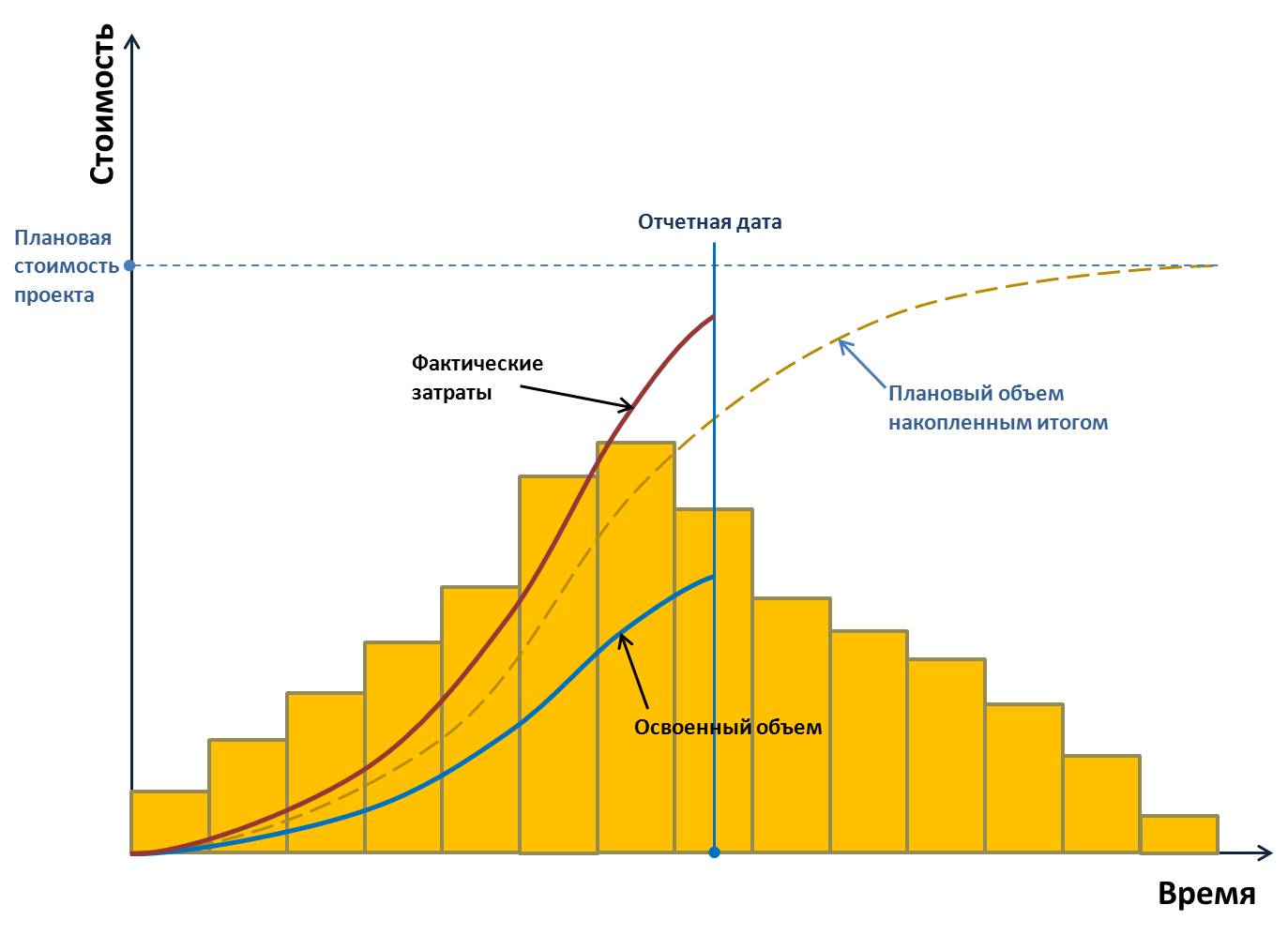
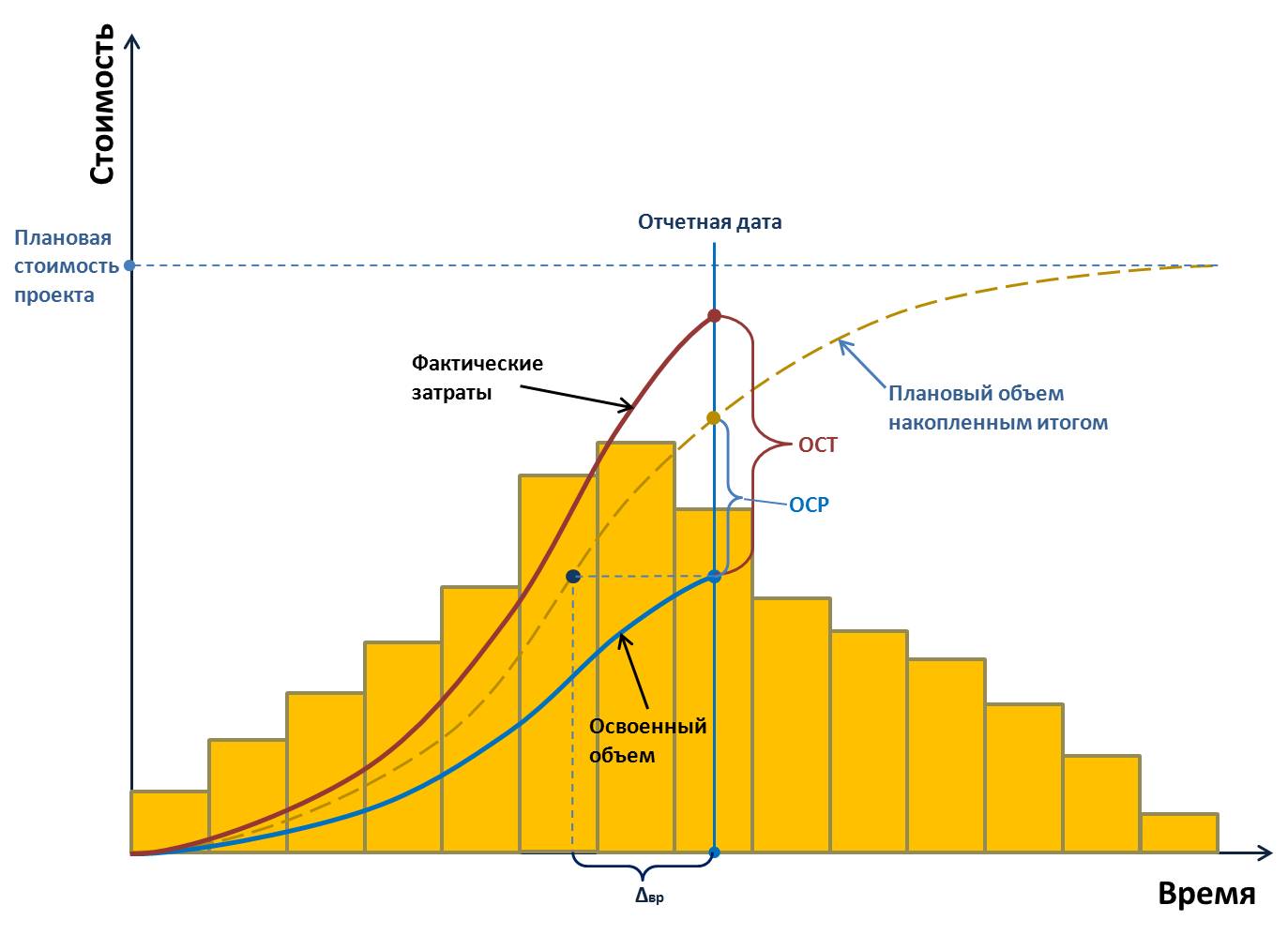
_<1>>=\frac<< _<2>>=\frac<< С какой производительностью работают две трубы вместе (не забывай, это задачи на совместную работу)? Берем количество литров, которое налила в бассейн первая труба за один час, прибавляем количество литров, которое налила в бассейн вторая труба за один час, – именно столько наливают в бассейн обе трубы за один час. То есть производительности складываются: То же самое, что и относительная скорость: с какой скоростью второй автомобиль приближается к первому? Со скоростью, равной сумме скоростей: \( \displaystyle v=< Тогда время, за которое с такой производительностью будет выполнена работа \( A\): При совместной работе производительности складываются Еще немного задач Пример №3 Заказ на \( \displaystyle 80\) деталей первый рабочий выполняет на \( \displaystyle 2\) часа дольше, чем второй. Сколько деталей за \( \displaystyle 1\) час делает первый рабочий, если известно, что второй делает за час на две детали больше, чем первый? Решение. Обычный способ Заказ на \( \displaystyle 80\) деталей первый рабочий выполняет на \( \displaystyle 2\) часа дольше, чем второй. Сколько деталей за \( \displaystyle 1\) час делает первый рабочий, если известно, что второй делает за час на две детали больше, чем первый? Мы получили систему уравнений: Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз: Решение. Альтернативный (продвинутый) способ Можно решить эту задачу быстрее, сразу перейдя к конечному уравнению, без составления системы. Мы уже знаем, что время в этой задаче нам находить не нужно. В условии есть \( \displaystyle A\) (работа), а нужно найти \( \displaystyle P\) (производительность). Так давай сразу выразим время! Предположим, рабочие начали делать работу одновременно, и после окончания хотят вместе пойти домой. Сколько на нее потратит первый? Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз: Пример №4 Первая труба пропускает на \( \displaystyle 5\) литров воды в минуту больше, чем вторая. Сколько литров воды в минуту пропускает вторая труба, если резервуар объемом \( \displaystyle 450\) литров она заполняет на \( \displaystyle 3\) минуты дольше, чем первая? Решение: У нас есть объем работы (\( \displaystyle 450\) литров) и нужно найти производительность. Давай выразим время, как и в предыдущей задаче. Время, за которое первая труба заполняет резервуар (\( \displaystyle < Поскольку нам нужно найти производительность второй трубы, обозначим её за \( \displaystyle x\) (давай привыкать делать так, как большинство математиков, а не использовать буквы из формулы). Тогда производительность первой трубы – \( \displaystyle x+5\). За сколько минут первая труба заполнит резервуар? Выражаем \( \displaystyle < Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз: Задачи на совместную работу отличаются от обычных, представленных выше, тем, что в них работа выполняется одновременно (совместно) несколькими рабочими (трубами и т.д.). В ЕГЭ задачи на совместную работу встречаются чаще, чем обычные, поэтому давай разбираться. Пример 5 Возьмем последнюю нашу задачу. Вторая труба пропускает \( \displaystyle 25\) литров в час, а первая \( \displaystyle \left( x+5 \right)=30\) литров в час. А за сколько времени они заполнят тот же резервуар, работая вместе? Первая труба пропускает \( \displaystyle 30\) литров в час, а вторая \( \displaystyle 25\) литров. За какое время они заполнят резервуар, объемом \( \displaystyle 450\) литров, работая вместе? Решение: Чему равна производительность первой трубы? \( \displaystyle 30\) литров в час. А второй? \( \displaystyle 25\). А сколько они будут наливать воды, если будут работать вместе? Очевидно что \( \displaystyle 30+25=55\). Ведь за \( \displaystyle 1\) час первая труба нальет \( \displaystyle 30\) литров, и за этот же час вторая нальет \( \displaystyle 25\) литров. Теперь мы можем легко найти искомое время: Ответ: \( \displaystyle \frac<90><11>\) На этом простом примере мы вывели главное правило совместной работы: При совместной работе производительности складываются. Теперь давай рассмотрим задачи посложнее. Пример 6 Две бригады, работая вместе, вспахали поле за \( \displaystyle 6\) часов. За сколько часов может вспахать поле первая бригада, работая самостоятельно, если ей необходимо на \( \displaystyle 5\) часов меньше, чем второй? Решение: Примем всю работу за \( \displaystyle 1\) (распространенный прием, ведь работа фиксированная, и не важно чему она равна). Пусть первая бригада может вспахать поле за \( \displaystyle x\) часов (обозначим именно этот показатель иксом, ведь именно его нас просят найти в задаче), тогда вторая вспашет это поле за \( \displaystyle \left( x+5 \right)\) часов. То есть их общая производительность была \( \displaystyle \frac<1> По условию сказано, что работая вместе, они вспахали поле за \( \displaystyle 6\) часов. То есть: Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз: Пример 7 Двое рабочих, работая вместе, могут выполнить работу за \( \displaystyle 15\) дней. За сколько дней, работая отдельно, выполнит эту же работу первый рабочий, если он за \( \displaystyle 4\) дня делает столько же, сколько второй за \( \displaystyle 5\) дней? Решение: Обозначим за \( \displaystyle < Нам нужно найти \( \displaystyle \frac<1><< Тогда по условию задачи: Кроме того, в условии сказано, что за \( \displaystyle 4\) дня первый рабочий делает столько же, сколько и второй за \( \displaystyle 5\) дней, то есть: Составим и решим систему: Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз: А теперь давай рассмотрим самый сложный пример, научившись решать который, ты сможешь с легкостью справится с любой задачей на ЕГЭ. Пример 8 На изготовление \( \displaystyle 600\) деталей первый рабочий тратит на \( \displaystyle 10\) часов меньше, чем второй рабочий на изготовление \( \displaystyle 500\) таких же деталей. За какое время, работая совместно, они изготовят партию в \( \displaystyle 1000\) деталей, если известно, что за час первый рабочий делает на \( \displaystyle 5\) деталей больше? Решение: Давай определимся, что нам нужно найти? Нам нужно найти время, за которое рабочие изготовят \( \displaystyle 1000\) деталей, то есть: \( \displaystyle \frac<1000><< _<1>>+< _<2>>>\). Значит, нужно найти \( \displaystyle < _<1>>\) и \( \displaystyle < _<2>>\). Первый рабочий за час делает на \( \displaystyle 5\) деталей больше. Обозначим производительность первого рабочего за х, тогда производительность второго – \( \displaystyle x-5\). \( \displaystyle 600\) деталей первый рабочий делает за \( \displaystyle < Приравняв \( \displaystyle < Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз: А теперь сам попробуй решить несколько задач, а затем проверь себя по ответам. Ответы: Курсы для тех, кому нужно получить 90+ и поступить в топовый ВУЗ страны. Сегодня ты научился решать задачи на работу. Чувствуешь себя увереннее? Напиши в комментариях, понравилась ли тебе статья! И какая часть тебе показалась интереснее. Аналогия с движением – классная штука, верно? 🙂 Если у тебя есть вопросы или предложения, тоже пиши их нижу в комментариях! Некоторые комментарии прошлых лет к этой статье: Елена Дамели Александр (админ) Софья Анастасия Написание данной статьи вызвано двумя причинами: Во-первых, незаслуженно малое внимание со стороны российских руководителей предприятий и менеджеров проектов к такому мощному инструменту управления как метод освоенного объема. Во-вторых, недостаток знаний в этом вопросе у большинства сотрудников и членов команд проектов не позволяет в полной мере использовать данный метод на исполнительском уровне с целью предоставления руководству качественной информации о состоянии проекта. Все это приводит к тому, что метод освоенного объема (МОО) зачастую воспринимается как нечто сложное, требующее специальной подготовки или, хуже того, как ненужные изыски в вопросах повышения эффективности управления проектами. Между тем МОО – это именно тот способ, который позволяет на самом высоком уровне очень наглядно показать состояние проекта с точки зрения ответа на вопрос “где мы находимся в проекте?”, т.е. удовлетворить главную потребность высшего руководства – понять ситуацию с проектом одним взглядом, причем в денежном выражении(!). Более того, МОО в состоянии показать это не только в статике, но и в динамике, т.е. продемонстрировать, как мы (компания, команда) пришли к такому состоянию и спрогнозировать к чему мы придем в дальнейшем, если предпримем/ не предпримем какие-то действия. Да, применение метода освоенного объема (МОО) требует от компании и команды проекта определенной управленческой, технической и методологической зрелости, но оно того стоит. Целью данной статьи является предоставление сотрудникам, занятым в реализации проектов (и особенно менеджерам) более или менее детальной инструкции по применению освоенного объема в своей работе, формирование понимания сути МОО и простых навыков интерпретации отчетов составленных с применением данного метода. По поводу освоенного объема написано немало теоретических и довольно скучных трудов, заставляющих читателя в большинстве случаев еще сильнее убедиться в сложности метода и окончательно охладеть к идее внедрения его в свою работу. Здесь мы постараемся максимально избежать этой теоретической скучности, но все же совсем без теории не обойтись. Итак, что же такое освоенный объем? В случае с одной работой, как в нашем примере, выяснить это совсем не сложно – достаточно посмотреть на физически выполненный объем работы. Если он составит запланированные 10м3, то налицо переплата денежных средств, а если 12м3, то очевидно, что на момент составления отчета имеет место опережение графика. Хуже, если выполненный объем будет меньше запланированных 10м3 (например, 9), тогда это означает не только переплату, но и отставание от графика. И наоборот: если выполненный объем больше 12м3, то это означает не только опережение графика, но и экономию средств. Представим эти варианты в табличной форме: Как видим, расчет освоенного объема позволяет однозначно интерпретировать состояние проекта, сравнивая между собой всего три величины. Очевидно, что при использовании освоенного объема, наличие в проекте любого количества работ, измеряемых в разных единицах, уже не является проблемой. Так как все три величины измеряются в деньгах, то их можно рассчитать для всего проекта в целом, просуммировав соответствующие значения, рассчитанные для каждой из работ. Удобство освоенного объема заключается также в том, что этот показатель позволяет оценить не только состояние всего проекта целиком, но и любой отдельно взятой его части, например, определенного вида работ или участка. С другой стороны данный показатель можно рассчитать и для более общей категории – всего портфеля проектов предприятия. Итак, теперь, рассчитав освоенный объем, мы знаем “где мы находимся” в проекте. Но, как мы увидим в дальнейшем, это только верхушка “айсберга полезности” освоенного объема. Следующие вопросы, которые мы должны себе задать – это насколько мы опережаем/отстаем или экономим/перерасходуем?, как мы пришли к этому состоянию?, как могут развиваться события в дальнейшем, если мы продолжим выполнять проект в рамках существующих тенденций? и как мы должны работать, для того, чтобы завершить проект в срок и в рамках бюджета? Об этом далее. Сам по себе освоенный объем позволяет констатировать факт нахождения проекта в определенном состоянии. Более детальный анализ этого состояния позволяют провести производные от него показатели. К простейшим показателям, рассчитываемым на основе освоенного объема, относятся: Первые два показателя являются абсолютными, вторые два – относительными. Показатель отклонения по срокам (ОСР) отражает отклонение от расписания, выраженное в деньгах (в дальнейшем будет понятно, как отклонение по срокам в деньгах отражает отклонение во времени) и рассчитывается следующим образом: ОСР = ОО-ПО. Очевидно, показатель ОСР будет отрицательным, если команда отстает по срокам от плана выполнения проекта. Величина ОСР покажет, сколько стоят те работы, которые команда проекта не успела выполнить на момент отчета. Аналогично показатель отклонения по стоимости (ОСТ) покажет отклонение от бюджета, запланированного на выполнение работ: ОСТ = ОО-ФС. Индексы выполнения сроков (ИВСР) и стоимости (ИВСТ) позволяют перейти от абсолютных показателей к относительным. Такой переход полезен для целей сравнения состояния различных проектов портфеля между собой, построения индикаторных диаграмм (светофоров и т.п.) и прогнозирования итогов проекта, т.к. фактически отражают накопленные тенденции в выполнении проекта. Индекс выполнения сроков сравнивает освоенный объем с плановым. Формула для его расчета: ИВСР = ОО/ПО. Значение ИВСР меньшее единицы указывает на задержки в выполнении работ. Индекс выполнения стоимости показывает эффективность финансовых затрат по проекту на текущий момент. Очевидно, что ИВСТ Графический смысл освоенного объема Если плановый объем (т.е. плановую стоимость работ) представить в разбивке по периодам (например, помесячно) в виде гистограммы, то для хорошо спланированного проекта мы получим нечто близкое к “горбу”, изображенному на рисунке ниже, а тот же самый плановый объем, но накопленным итогом, изобразиться на графике в форме кривой. Эту кривую также принято называть S-кривая. S-кривая показывает, как, в соответствии с исходным планом, должен осваиваться бюджет проекта. В самом деле: если в начале проекта преобладают недорогие подготовительные и прочие “начальные” работы и S-кривая имеет небольшую скорость роста, то в самый разгар проекта выполняется наибольший и самый дорогой объем работ, в результате чего в этом время S-кривая имеет наибольшую скорость роста. По мере продвижения проекта “вправо” основные объемы постепенно завершаются, а скорость роста S-кривой падает. Именно так проект должен развиваться по плану. Но, как известно в реальной жизни всегда имеют место некоторые отклонения. Рассмотрим их. Предположим, что некий проект отстает от графика по срокам, а фактические затраты на выполнение работ при этом превышают плановые. Тогда выбрав некоторую отчетную дату на графике и построив кривую освоенного объема и фактических затрат (также накопленным итогом) увидим следующую картину: Как видно из графика кривые планового и освоенного объемов, а также фактических затрат очень наглядно отражают состояние проекта на отчетную дату с точки зрения недоосвоения бюджета и перерасхода денежных средств. Что мы видим? Что в некоторый момент времени плановая стоимость выполненных работ “не дотягивает” до требуемого уровня, при этом фактические затраты понесенные по проекту уже значительно превышают плановые. Заметим, что уже знакомые нам показатели отклонения по срокам и стоимости также видны на этом графике особенно наглядно: Более того, к наглядности денежных показателей отклонений добавилось еще и отражение временной задержки проекта: величина Δвр показывает, насколько проект отстает от плана во времени. Данный показатель можно интерпретировать еще и следующим образом: Именно такое графическое представление освоения планового объема и показывает, как было обещано выше, не только состояние проекта в некоторый фиксированный момент времени, но и то, “как проект к этому пришел”. Не правда ли, достаточно одного взгляда на подобный график, чтобы понять насколько хорошо “чувствует себя” проект? В совокупности с данными из последней приведенной таблицы руководство предприятия или заказчик проекта имеют перед глазами короткий, но очень наглядный отчет, отражающий состояние проекта. Однако это все же только состояние. Поэтому вопросы наши не заканчиваются. Следующие вопросы, как не трудно догадаться звучат так: Что будет с проектом дальше, если мы продолжим выполнять проект в том же духе? и Как мы должны работать над проектом дальше, чтобы завершить его выполнение в срок и в рамках согласованного бюджета.Читать далее…
Читать далее…
Читать далее…
Разбор задач на совместную работу
Читать далее…
Читать далее…
Читать далее…
Задачи для самостоятельного решения
Наши курсы по подготовке к ЕГЭ по математике, информатике и физике
Теперь дело за тобой!
Добавить комментарий Отменить ответ
Один комментарий
16 января 2020
очень интересное изложение материала
17 января 2020
Все очень понятно спасибо
05 февраля 2020
Да не за что, Владимир 🙂
03 июня 2020
Все просто и кратко. Благодаря вам я наконец изучила и закрепила то, что до этого не понимала. Спасибо за труд! Объяснение лучше математички 🙂
05 июня 2020
спасибо за прекрасное объяснение! как будто сидела перед Вами, когда задавали вопросыМетод освоенного объема в управлении проектами
Введение
Часть I. Формирование отчета о состоянии проекта
Немного теории
Работа Длительность, дн. Объем, м3 Стоимость, $ Выкапывание колодца 100 100 100 000 Отставание от графика и перерасход Отставание от графика Все по плану $9000 $9000 = $9000 Все по плану = $10000 = $10000 Перерасход денежных средств = $10000 $12000 Показатели, рассчитываемые на основе освоенного объема