Если с увеличением значения аргумента значение функции растет то говорят что функция

Если с увеличением значения аргумента значение функции растет то говорят что функция

Основные понятия.

Функция (или Функциональная зависимость) – это зависимость переменной y от переменной x. Это такая зависимость, при которой каждому значению переменной x соответствует только одно значение переменной y.

Переменную x называют независимой переменной или аргументом.

Переменную y называют зависимой переменной или функцией от переменной x.

Значение независимой переменной называют абсциссой (горизонтальная плоскость графика).

Соответствующее значение зависимой переменной называется ординатой (вертикальная плоскость графика).

Совокупность значений независимой переменной называется областью определения функции.

Совокупность значений зависимой переменной называют областью значений функции.

График функции – это множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции.

Значения аргумента, при которых функция обращается в нуль, называют нулями функции.

То есть в этой точке кривая имеет координаты (-2;0):

Этот аргумент и называется нулем рассматриваемой функции.

Если кривая на оси координат возрастает, то это означает, что с увеличением значения аргумента увеличивается и значение функции. Такая функция называется возрастающей.

Если кривая убывает, то это означает, что с увеличением значения аргумента значение функции убывает. Такая функция называется убывающей.

Виды функций.

Существует несколько основных видов функций:

Графики функций.

Графиком линейной функции y = kx + b является прямая.

Графиком прямой пропорциональности y = kx является прямая, проходящая через начало координат.

k
Графиком обратной пропорциональности y = — является гипербола.
x

Графиком квадратичной функции y = x 2 является парабола.
Если х = 0, то у = 0.
Если х ≠ 0, то у > 0.

Подробнее о приведенных и других функциях – в следующих разделах.

Источник

Реальный мир

Рис.6. Соотношение модели и реального мира

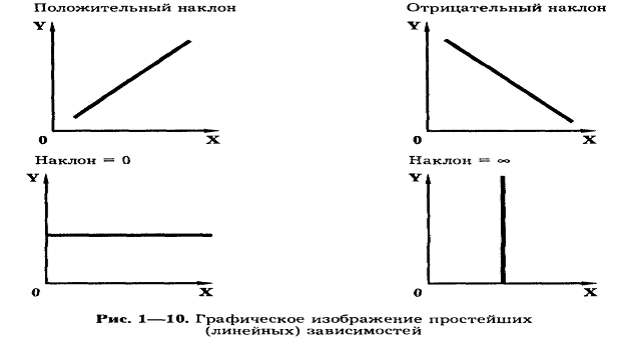
Простейшим видом экономико-математическогомоделирования является моделирование в двухмерном пространстве—при помощи графиков. Если с увеличением значения аргумента значение функции ли и реального растет, наклон графика называют положительным, если с увеличением значения аргумента значение функции уменьшается, наклон называют отрицательным. Если с изменением значения аргу­мента значение функции не меняется, то говорят, что у функции нулевой наклон. Если, наконец, одному и тому же значению аргумента соответствует бесконечное число значений функции, то наклон функции равен бесконечности (рис. 7).

Положительный наклон отрицательный наклон

Y y

0 x0 x

. наклон=бесконечность

0 х 0 х

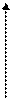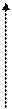Рис.7. Графическое изображение простейших (линейных) зависимостей

На микроуровне На макроуровне

1. Р.Оуэн 1. Народнохозяйственное

2. Ф.Тейлор планирование в СССР

3. Г.Форд 2. Кейнсианские эксперименты

4. Э.Мейо и др. 3. Политика монетаризма и др.

Рис. 8. Виды экспериментов

Сознательное массовое экономическое экспериментирование — порождение XIX в. Наиболее известные экономические эксперименты, проведенные на микроуровне, связаны с деятельностью Р. Оуэна, «банками справедливого обмена» П.Ж. Прудона, а также с теоретиками научной организации труда Ф. Тейлором, Г. Фордом и Э. Мейо. Широкие эксперименты на макроуровне проводились в СССР с первых лет советской власти. На Западе они связаны, прежде всего с именами Дж. М. Кейнса, М. Фридмена и их последователей. В последующий период роль экономических экспериментов заметно возросла, и в настоящее время серьезная, научно обоснованная поли­тика немыслима без проведения широких и разнообразных эко­номических экспериментов. Экономические эксперименты позволяют на практике проверить обоснованность тех или иных экономических рекомендаций и программ, не допустить крупных народнохозяйственных ошибок и провалов.

Экономические цели. Здесь важно отметить и осмыслить ряд экономических целей или цепочных суждений, которые широко, хотя и не всеми, признаны в нашем обществе, а по существу, и во многих других обществах. Эти цели можно кратко сформулировать следующим образом:

1. ЭКОНОМИЧЕСКИЙ РОСТ. Желательно обеспечить производство большего количества и лучшего качества товаров и услуг, а проще говоря — более высокий уровень жизни.

2. ПОЛНАЯ ЗАНЯТОСТЬ. Подходящее занятие следует обеспечить всем, кто желает и способен работать.

3. ЭКОНОМИЧЕСКАЯ ЭФФЕКТИВНОСТЬ. Мы хотим получить максимальную отдачу при ми­нимуме издержек от имеющихся ограниченных про­изводственных ресурсов.

4. СТАБИЛЬНЫЙ УРОВЕНЬ ЦЕН. Необхо­димо избегать значительного повышения или сни­жения общего уровня цен, то есть инфляции и де­фляции.

5. ЭКОНОМИЧЕСКАЯ СВОБОДА. Управля­ющие предприятиями, рабочие и потребители долж­ны обладать в своей экономической деятельности высокой степенью свободы.

6. СПРАВЕДЛИВОЕ РАСПРЕДЕЛЕНИЕ ДО­ХОДОВ. Ни одна группа граждан не должна пребы­вать в крайней нищете, когда другие граждане купа­ются в роскоши.

7. ЭКОНОМИЧЕСКАЯ ОБЕСПЕЧЕННОСТЬ. Следует обеспечить существование хронически больных, нетрудоспособных, недееспособных, пре­старелых или других иждивенцев.

8. ТОРГОВЫЙ БАЛАНС. Мы стремимся к под­держанию разумного баланса нашей международ­ной торговли и международных финансовых сделок.

Этот перечень широко признанных целей созда­ет базу для постановки ряда существенных вопро­сов. Во-первых, отметим, что это или любое иное изложение основных экономических целей неизбеж­но влечет за собой проблему их толкования. Каковы значительные изменения уровня цен? Что такое высокая степень экономической свободы? Что та­кое «справедливое» распределение доходов? Хотя большинство из нас готово согласиться с приведен­ными выше целями в их общей формулировке, мы можем вместе с тем существенно разойтись во мне­ниях относительно их конкретного толкования, а следовательно, и относительно специфических по­литических программ, необходимых для достиже­ния этих целей. Заслуживает внимания то обсто­ятельство, что если цели 1—4 и 8 поддаются доволь­но точному измерению, то невозможность количест­венно измерить цели 5—7, несомненно, способствует возникновению споров относительно их точного значения. Во-вторых, некоторые из этих целей взаимодопо­лняемы в том смысле, что по мере достижения одной из них другая или другие цели также могут быть осуществлены. Например, достижение полной заня­тости (2-я цель) явно означает ликвидацию безрабо­тицы, то есть основной причины низких доходов (6-я цель) и экономической необеспеченности (7-я цель). Кроме того, анализ 1-й и 6-й целей приводит к обще­признанному заключению, что социополитические напряжения, которые может вызывать резкое нера­венство в распределении доходов, ослабляются по мере увеличения абсолютных размеров большинст­ва доходов в результате экономического роста. В-третьих, некоторые цели могут противоречить друг другу или взаимно исключать друг друга. Не­которые экономисты утверждают, что те силы, ко­торые способствуют достижению экономического роста и полной занятости, могут оказаться теми самыми силами, которые порождают инфляцию. В самом деле, в последние годы в центре внимания экономических исследований и дискуссий оказалось явное противоречие между 2-й и 4-й целями. Могут также противоречить друг другу 1-я и 6-я цели. Ряд экономистов отмечает, что стремление осуществить большее равенство в распределении доходов может ослабить стимулы к труду, к инвестированию, тех­ническому прогрессу и предпринимательскому рис­ку, то есть ослабить действие именно тех факторов, которые способствуют быстрому экономическому росту. Они выдвигают аргумент, что правительство склонно выравнивать распределение доходов путем введения весьма больших налогов на лиц с высо­кими доходами и передачи поступлений от таких налогов лицам с низкими доходами. Стимулы для человека с высоким доходом ослабляются тем, что такое налогообложение сокращает возможность пользоваться плодами высокого дохода. Аналогич­но этому у человека с низким доходом имеются меньшие стимулы к труду и к тому, чтобы заняться другим видом производительной деятельности, ког­да правительство выражает готовность его субсиди­ровать. Приведем пример из международной сферы. На основе централизо­ванного планирования Советский Союз сумел прак­тически ликвидировать безработицу, в результате чего этот источник незащищенности рабочего почти исчез. Однако, избавившись от страха потерять ра­боту, советские рабочие стали довольно небрежно относиться к выполняемой работе, и поэтому произ­водительность труда и эффективность производства в Советском Союзе очень низкие. Здесь мы наблю­даем противоречие между 7-й целью (экономичес­кой обеспеченностью) и 1-й целью (ростом произ­водительности рабочих). Это приводит нас к четвертому заключению. Когда основные цели вступают в противоречие друг с другом, общество вынуждено разработать систему приоритетов в осуществлении задач, которые оно перед собой ставит. Проиллюстрируем это на следу­ющем примере : если такие цели, как полная заня­тость и стабильный уровень цен в какой-то степени взаимно исключают друг друга, то есть если полная занятость сопровождается некоторой инфляцией, а стабильный уровень цен влечет за собой некото­рую безработицу, общество должно решить, какую из этих целей оно считает относительно более важ­ной. Предположим, что предстоит выбрать между двумя вариантами, скажем между сопровождаемым полной занятостью увеличением годового уровня цен на 7°/с. с одной стороны, и совершенно стабиль­ным уровнем цен при 8-процентной доле безработи­цы — с другой. Какой вариант предпочтительнее? А как отнестись к компромиссной цели в форме, скажем, 4-процентного годового роста уровня цен при 6-процентной доле безработицы? Здесь, разуме­ется, открывается широкое поле для разногласий. Разработка экономической политики. Выработка конкретных программ достижения крупных эконо­мических целей нашего общества представляется далеко не простым делом.

Кратко рассмотрим основные этапы подготовки такой политики. 1. Первый шаг заключается в том, чтобы дать четкое определение целей. Если мы утверждаем, что и имеем «полную занятость», означает ли это, что каждый человек в возрасте от 16 до 65 лет имеет работу? Или означает ли это только то, что каждый, кто хочет трудиться, имеет работу? Следует ли допускать возможность какого-то «нормального» уровня безработицы, существующей вследствие добровольной смены рабочими своего места работы?

3. Мы обязаны как для самих себя, так и для будущих поколений изучить прошлый опыт реали­зации подобных программ и ценить их эффектив­ность; только путем такой оценки можно рассчиты­вать на повышение результативности политики. Привело ли то или иное изменение политики нало­гообложения или массы денег в обращении к изме­нению уровня занятости в первоначально предска­занных размерах? Привело ли дерегулирование от­дельной отрасли (например, авиаперевозок) к пред­сказанным благотворным результатам? Если нет, то почему?

Источник

Свойства функции. Возрастание и убывание, наибольшее и наименьшее значения, нули, промежутки знакопостоянства.

теория по математике 📈 функции

Каждый из нас встречался с разными графиками, как на уроках, так и в жизни. Например, рассматривали, как изменяется температура воздуха в определенный период времени.

На рисунке видно, что температура воздуха была отрицательной с 0 часов до 6 часов, а также с 20 до 24 часов. Еще можем сказать, что температура повышалась до 14 часов, а затем понижалась. То есть по данному графику мы смогли определить некоторые свойства зависимости температуры воздуха от времени суток.

Остановимся подробнее на свойствах функций.

Нули функции

Нули функции – это значение аргумента, при которых функция обращается в нуль. Если смотреть нули функции на графике, то берем точки, где график пересекает ось х.

На рисунке он пересекает ось х при х=-1; х=4; х=6. Эти точки пересечения выделены красным цветом. Внимание!

Существует функция, которая не будет иметь нули функции. Это гипербола. Вспомним, что функция имеет вид у=k/x, где х не равное 0 число.

а) Для нахождения нулей функции необходимо в данную формулу вместо у подставить число 0, так как координаты точки пересечения графика с осью х (х;0). Нам нужно найти значение х. Получаем 0 = –11х +12. Решаем уравнение. Переносим слагаемое, содержащее переменную, в левую часть, меняя знак на противоположный: 11х=22

Находим х, разделив 22 на 11: х=22:11

Таким образом, мы нашли нуль функции: х=2

Пример №2. Найти нули функции у=f(x) по заданному графику.

Находим точки пересечения графика с осью х и выписываем значения х в этих точках. Это (-4,9); (-1,2); 2,2 и 5,7. У нас на рисунке точки пересечения выделены красным цветом.

Промежутки знакопостоянства

Промежутки, где функция сохраняет знак (то есть значение y либо положительное на этом промежутке, либо отрицательное), называется промежутками знакопостоянства.

Пример №3. Найдем промежутки знакопостоянства по заданному на промежутке [-2; 10] графику функции у=f(x).

Функция принимает отрицательные значения в промежутках (-1; 3) и (8; 10]. Обратите внимание на линии синего цвета.

Возрастание и убывание функции

Значения функции могут уменьшаться или увеличиваться. Это зависит от того, как изменяются значения х. Рассмотрим это свойство по рисунку.

Посмотрим на значения х, которые увеличиваются от 2 до 5. В этом случае значения у уменьшаются. На графике эта часть выделена зеленым цветом. Слева направо эта часть графика идет вниз. То есть в промежутке [2;5] функция у=f(x) является убывающей.

Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции; функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.

Источник

Возрастание и убывание функции

Общие понятия о поведении функций

Исследуя функции, заданные определенными уравнениями, особенно уделяют внимание их свойствам, а именно возрастанию или убыванию.

Монотонной функцией называется функция, меняющаяся в одном направлении.
На графиках представлены примеры монотонно возрастающей и монотонно убывающей функций.

Соответственно, монотонная функция может быть возрастающая или убывающая.

Возрастающей называется такая функция, у которой при увеличении значения аргумента, значение функции увеличивается, иными словами, чем больше значение аргумента, тем больше значение функции.

Математическое выражение этого определения выглядит следующим образом:

Убывающей называется такая функция, у которой при увеличении значения аргумента, значение функции уменьшается, иными словами, чем больше значение аргумента, тем меньшее значение функции.

Математическое выражение этого определения выглядит следующим образом:

Разберем примеры решения задач на изучение характера поведения функции.

Поскольку значения функции увеличиваются, при увеличении значений аргумента, то данная функция на заданном отрезке будет возрастать.

Поскольку значения функции уменьшаются, при увеличении значений аргумента, то данная функция на данном отрезке будет убывать.

Не возрастающей называется такая функция, у которой при увеличении значения аргумента, значение функции увеличивается или остается на том же уровне, иными словами, большему значению аргумента соответствует большее или равное значение функции.

Не нашли что искали?

Просто напиши и мы поможем

Не убывающей называется такая функция, у которой при увеличении значения аргумента, значение функции уменьшается или остается на том же уровне, иными словами, большему значению аргумента соответствует меньшее или равное значение функции.

Постоянной называется такая функция, которая не убывает и не возрастает, то есть при увеличении или при уменьшении значения аргумента, значение функции остается на одном и том же уровне. Пример такой функции можно наблюдать на рисунке.

То есть функция \(y=5\) будет постоянной.

Постоянная, не убывающая и не возрастающая функции не есть монотонные.

Свойства монотонных функций

К свойствам монотонных функций относятся такие характеристики:

Монотонность производной и заданной функций связаны между собой, и это описано в таких теоремах:

Источник

Экономические модели и эксперименты

В начале XX в. А. А. Богданов(1873—1928) попытался создать всеобщую организационную науку —тектологию, которая, по мысли ее творца, как и математика, отвлекается от конкретного характера элементов системы, изучая их с точки зрения организованности или дезорганизованности. Это позволяет объединить на основе общего строения социально-экономические, энергетические и биологические процессы. В основе такого объединения лежит идея равновесия: статического и динамического. В соответствии с этим подходом А. Богданов делил все системы на уравновешенные и неуравновешенные.

Мощным импульсом для развития экономического моделирования стали теория и практика народнохозяйственного планирования в СССР (ГОЭЛРО, межотраслевой баланс 1923—1925 гг., модели экономического роста Г. А. Фельдмана и др.). В 1939 г.

Л. В. Канторовичсоздал метод линейного программирования. Развитие технических наук (теории машин и механизмов, теории связи и информации), математики (теории алгоритмов, математической логики, теории вероятностей, математического программирования), а также биологии и физиологии (исследование систем регулирования в живых организмах, учение И. П. Павлова о высшей нервной деятельности и т. д.) способствовало возникновению во второй половине 40-х гг. кибернетики.

«Отцом» новой науки стал американский исследователь Н. Винер.Кибернетика возникла как наука об управлении сложными динамическими системами (независимо от того, является ли такая система механической конструкцией или живым организмом). Применение кибернетических принципов к экономике увенчалось в начале 60-х гг. созданием экономической кибернетики (В. С. Немчинов, О. Ланге, Г. Греневский, С. Вир и др.).

Распространение системных методов исследования и рождение кибернетики сопровождались бурным развитием экономико-математического моделирования.

Экономическая модель — это формализованное описание экономического процесса или явления, структура которого определяется как его объективными свойствами, так и субъективным целевым характером исследования.

Создание модели связано с потерейчасти информации. Это позволяет абстрагироваться от второстепенных элементов, сконцентрировать внимание на главных элементах системы и их взаимосвязи. Известные величины, вводимые в модель в готовом виде, называются экзогенными; величины, которые получаются в рамках модели при решении поставленной задачи, называются эндогенными.

Связь модели с объективной экономической действительностью двояка: с одной стороны, модель отражает реальный мир, является его условным воспроизведением, с другой — служит его преобразованию в соответствии со сформулированными целями.

Простейшим видом экономико-математического моделирования является моделирование в двухмерном пространстве — при помощи графиков.

Если с увеличением значения аргумента Х значение функции У растет, наклон графика называют положительным,

Если с увеличением значения аргумента значение функции уменьшается, наклон называют отрицательным.

Если с изменением значения аргумента значение функции не меняется, то говорят, что у функции нулевой наклон.

Если, наконец, одному и тому же значению аргумента соответствует бесконечное число значений функции, то наклон функции равен бесконечности (см. рис. 1—10).

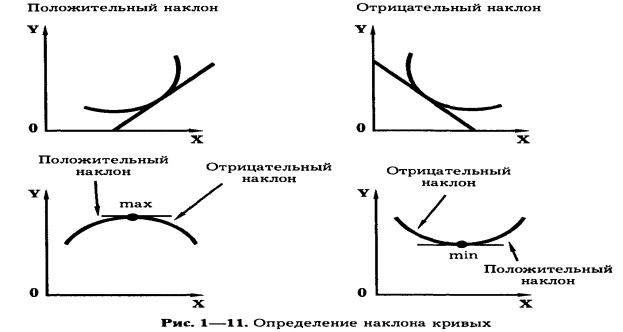
На рис. 1—10 показаны простейшие линейные зависимости; однако в реальной действительности зависимости носят более сложный характер и изображаются кривыми. Чтобы определить уровень наклона функции в окрестностях данной точки, необходимо к ней провести касательную так, как показано на рис. 1—11. Кроме того, наклон функций может меняться, переходя из положительного в отрицательный и наоборот.

Мир моделей многообразен. Они различаются по уровню обобщения (абстрактно-теоретические и конкретно-экономические), сфере охвата (макро- и микроэкономические), времени и характеру действия (статические и динамические), степени структурализации (малоразмерные и многоразмерные), характеру взаимосвязи элементов (линейные и нелинейные) и т. д. Наибольшее значение в экономической науке играет микро- и макромоделирование.

Предпосылки для возникновения микроэкономики складываются во второй половине XIX в., когда в экономической науке все большее внимание начинает уделяться психологическому фактору. Австрийская школа предельной полезности стала рассматривать в качестве исходного пункта экономической науки автономного индивида, независимого от окружающего мира. Основная задача его деятельности — удовлетворение потребностей в условиях ограниченности ресурсов. Поведение этого индивида рассматривается в различных гипотетических ситуациях с целью выбора оптимального варианта (теория выбора А. Маршалла). При этом предполагается почти полная взаимозаменяемость факторов (труда, капитала и т. д.).

Экономическая наука выступает при таком подходе как сборник готовых рецептов поведения индивида, фирмы и т. д. в стандартных ситуациях, как нормативная наука. Специфически капиталистическое выдается за общечеловеческое, рыночная экономика — за экономику вообще. При таком подходе неизбежно представление о современном обществе как о наилучшем, как о самой гармоничной системе.

Крах золотомонетного стандарта после 1914 г., а затем Великая депрессия 1929—1933 гг. наглядно обнажили несовершенство функционирующей системы. Возникла необходимость возвращения к объективному подходу, типичному для предшествовавшей экономической теории, рассмотрению функционирования народного хозяйства как единого целого (макроэкономика).

Это достигается, во- первых, в анализе таких категорий, как национальный доход, сбережения, инвестиции и моделирование взаимосвязей между ними; во-вторых, путем значительного расширения эмпирической базы и совершенствования экономико-математических методов их обработки (развитие эконометрики, кибернетики и т. д.). Причинно-следственные связи вытесняются функциональными и структурными, происходит четкое разграничение микро- и макроэкономики.

Изучение естественного хода явлений и процессов экономической жизни ставит на повестку дня проведение экспериментов.

Сознательное массовое экономическое экспериментирование — порождение XIX в. Наиболее известные экономические эксперименты, проведенные на микроуровне, связаны с деятельностью Р. Оуэна, «банками справедливого обмена» П. Ж. Прудона, а также с теоретиками научной организации труда, производства и управления — Ф. Тейлором, Г. Фордом и Э. Мейо.

Широкие эксперименты на макроуровне проводились в СССР с первых лет советской власти. На Западе они связаны прежде всего с именами Дж. М. Кейнса, М. Фридмена и их последователей.

В последующий период роль экономических экспериментов заметно возросла, и в настоящее время серьезная, научно обоснованная политика немыслима без проведения широких и разнообразных экономических экспериментов.

Экономические эксперименты позволяют на практике проверить обоснованность тех или иных экономических рекомендаций и программ, не допустить крупных народнохозяйственных ошибок и провалов.

Источник