За счет чего достигается портфельный эффект
Портфельный эффект и гримасы корреляции
Почему не стоит полагаться на корреляции при выборе активов в портфель. И на доходности тоже.
Портфельный эффект — это несводимость доходности и риска портфеля к взвешенной сумме доходностей и рисков его составляющих.
а риск (понимаемый как СКО/дисперсия периодических доходностей) — уменьшается:
Здесь активы повторяют динамику друг друга с небольшим смещением.
Я думаю, вы уже догадались, что я буду предлагать против этой проблемы, но посмотрим ещё на несколько примеров.
Про раскоррелированные я уже и не говорю, тут даже очень большой волатильности не нужно, чтобы большой минус (−5%г) превратить в достойный плюс (+2%г):
Таким образом, ни значение коэффициента корреляции между доходностями активов, ни ожидаемые значения самих этих доходностей не могут служить основанием не включать активы в портфель (или, наоборот, включать).
А что же делать с корреляциями?
Здесь я выкладываю лишь собственные размышления/исследования/расчёты, иногда собственное же изложение чужих мнений или результатов исследований. Размещённая информация может содержать ошибки, быть неактуальной на момент прочтения, допускать множество интерпретаций и проч. Я не занимаюсь образовательной деятельностью и не даю инвестиционных рекомендаций ни на этом сайте, ни в частном порядке.
Может быть, вам показалось, но способов получить гарантированную доходность за счёт каких бы то ни было финансовых инструментов, портфелей или торговых стратегий НЕ СУЩЕСТВУЕТ. Хуже того, способов гарантированно сохранить свой капитал тоже НЕ СУЩЕСТВУЕТ.
Материалы сайта могут быть использованы на условиях лицензии CC BY-NC-SA.
© Андрей Болкисев, 2021.
Asset Allocation: портфельный эффект
Автор: Алексей Мартынов · Опубликовано 30.05.2016 · Обновлено 04.06.2016
В предыдущих статьях, посвященных Asset Allocation, были описаны важные вещи: диверсификация, корреляция активов, их риск и доходность. Но это только присказка. В этой статье вы узнаете, как все это объединяется и работает в единой инвестиционной стратегии, что такое портфельный эффект и как он возникает. А так же, как составить инвестиционный портфель, чтобы увеличить его доходность и снизить риск. Для начала вспомним основные моменты.
При выборе активов в портфель нужно помнить четыре правила:
Что такое портфельный эффект?
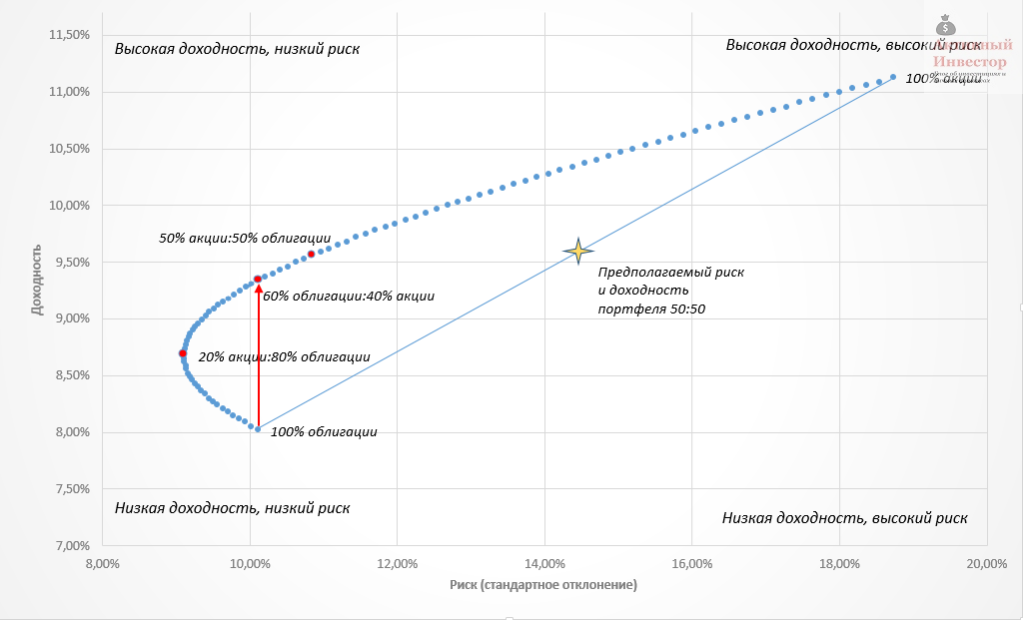
Только грамотно составленный инвестиционный портфель сможет сгенерировать то, что называет портфельный эффект. Если взять два актива — акции и облигации США и составить из них множество портфелей с разными пропорциями, то доходность и риск портфелей на диаграмме будет выглядеть в виде кривой, которая называется границей эффективности Марковица. На горизонтальной оси представлен риск (стандартное отклонение), на вертикальной — средняя годовая доходность. Точки на линии представляют различные варианты распределения активов в портфеле, начиная от 100% акций до 100% облигаций. Множество точек образует кривую со всевозможным сочетанием пропорций активов в портфеле. В зависимости от распределения активов и выбранных классов активов эта кривая может изгибаться.
Граница эффективности портфеля
Как видно, портфель, состоящий на 100% из облигаций продемонстрировал низкую доходность и низкий риск, а портфель из акций наоборот — высокую доходность при высоком риске.На первый взгляд, портфель в пропорции 50:50 по риску и доходности должен оказаться посередине прямой линии, проведенной между крайними точками. Но в реальности риск такого портфеля оказался значительно ниже. Такой эффект возник в результате ребалансировки портфеля.
Важно отметить, что портфель в пропорции 20% акции:80% облигации оказался менее рискованным, чем 100% облигации, при этом продемонстрировал на доходность на 1,5% больше. Таким образом можно придти к удивительному выводу, что добавление более рискованного актива уменьшило риск портфеля и увеличило его доходность.
Так же можно заметить, что портфель 60% облигации:40% акции по риску был аналогичен портфелю из 100% облигаций, но принес более высокую доходность на 2%. То есть добавление в портфель рискованного актива значительно увеличило его доходность, при этом нисколько не увеличив риск.
Диаграмму можно условно поделить на 4 квадрата, каждый из которых можно описать сочетанием риска и доходности. Например, Нижний правый квадрат — это высокий риск и низкая доходность, а Верхний правый квадрат — высокий риск и высокая доходность. Наиболее предпочтительным является верхний левый квадрат, где высокая доходность сочетается с низким риском. Именно в этой области лежат самые эффективные портфели. А самым нежелательным квадратом является правый нижний, где низкая доходность и высокий риск.
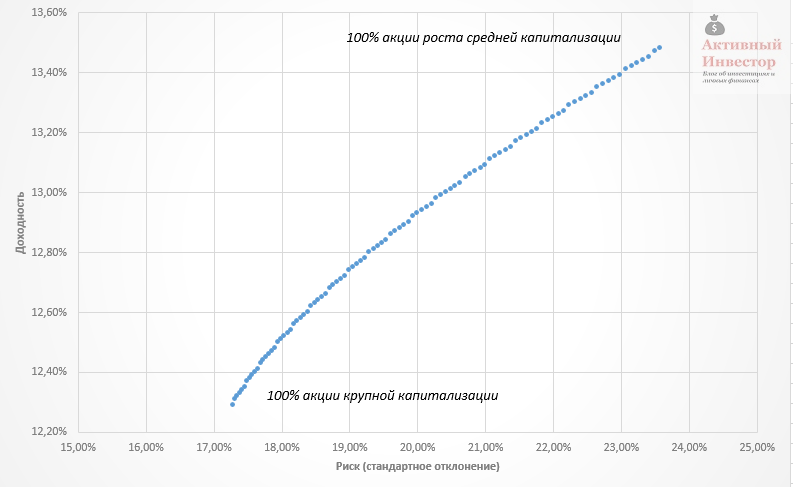
Портфельный эффект возникает не всегда: все зависит от подобранных активов. Например, портфель, состоящий из акций крупной капитализации США и акций роста средней капитализации не генерирует портфельного эффекта. Эти активы слишком похожи друг на друга, поэтому ведут себя почти одинаково и имеют высокую корреляцию.
Рассмотренные примеры выше включали только два класса активов: акции и облигации США. Но не стоит ограничиваться только ими. Есть еще такие классы как недвижимость и товарные активы. Кроме того акции и облигации делятся на большое количество подклассов. Посмотрим, как влияет на риск и доходность портфеля добавление в него более двух классов активов.
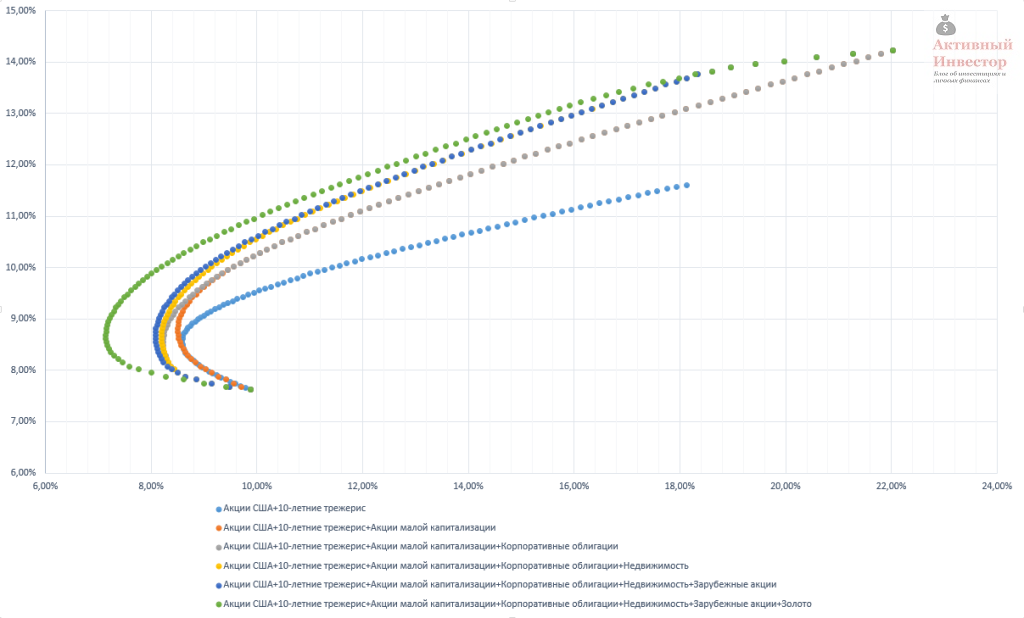
Ниже на диаграмме представлены границы эффективности портфелей за период с 1973 по 2015 год. В каждый следующий портфель добавляется какой-то новый актив. Например, первый портфель включает только два актива: акции и облигации США, во второй к этим двум активам прибавлен третий — акции малой капитализации США, в третий портфель добавлены корпоративные облигации и так далее. Последний, шестой по счету портфель, включает 7 классов активов.
Граница эффективности портфелей 1973-2015
Можно заметить, что с включением каждого нового актива граница эффективности портфеля смещается влево. Если взять и сравнить риск первого и шестого портфелей, то окажется, что при одинаковой доходности 9%, стандартное отклонение первого портфеля составило 8,88%, а шестого 7,2%. То есть с включением в портфель каждого нового класса активов его риск уменьшался, а доходность как минимум не падала.
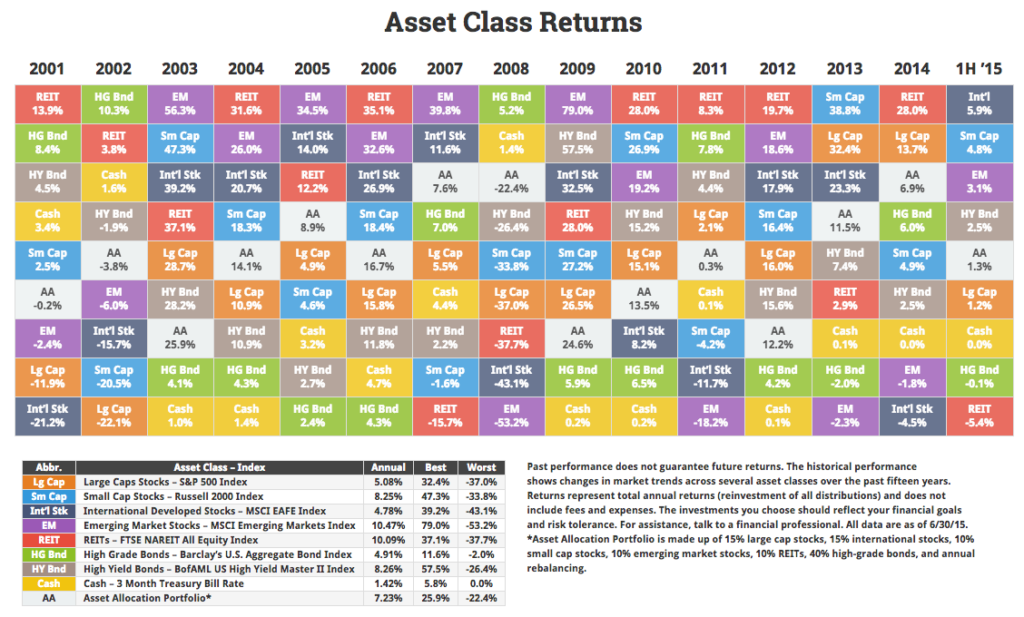
Пример поведения портфеля Asset Allocation
Если взять не теоретическую модель, а реальный портфель, который бы включал разные классы активов, то оценить его динамику можно на следующей диаграмме. На ней изображены годовые доходности различных классов активов: акции крупной и малой капитализации США (Lg Cap, Sm Cap), акции развитых и развивающихся стран (Intn`l Stk, EM), недвижимость (REIT), высоконадежные и высокодоходные облигации США (HG Bnd и HY Bnd), 3-месячные казначейские векселя (Cash). Так же на диаграмме присутствует портфель Asset Allocation (AA), который состоит из этих активов. Структура портфеля: 15% Lg Cap, 15% Intn`l Stk, 10% Sm Cap, 10% EM, 10% REIT, 40% HG Bnd с ежегодной ребалансировкой.
Портфели из разных классов активов
Теперь посмотрим, как включение того или иного класса активов может влиять на риск и доходность портфеля.
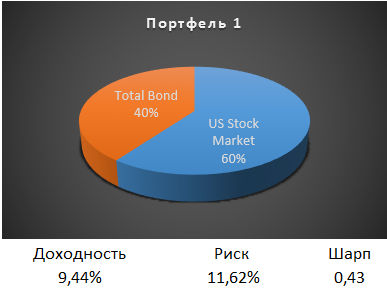
Для начала возьмем самый простой портфель из 60% акций США и 40% облигаций США. На промежутке с 1972 по 2015 такой портфель принес среднюю доходность 9,44% при стандартном отклонении 11,62%. Чтобы оценить соотношение риска и доходности портфеля будем использовать коэффициента Шарпа. Чем он больше, тем лучше это соотношение. У данного портфеля коэффициент Шарпа составил 0,43.
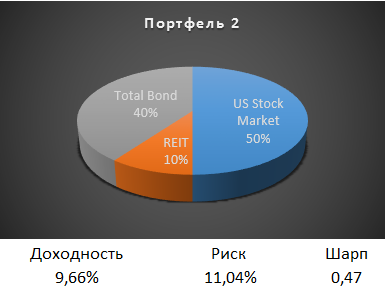
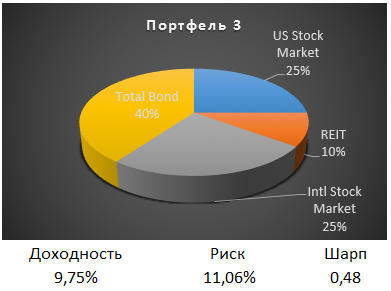
Доходность такого портфеля на 0,09% больше предыдущего, а риск вырос на 0,02%. Коэффициент Шарпа 0,48.
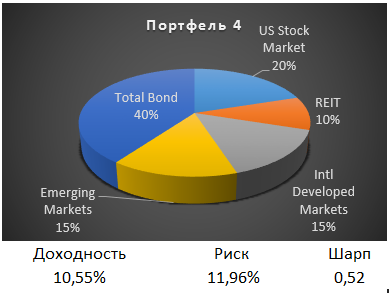
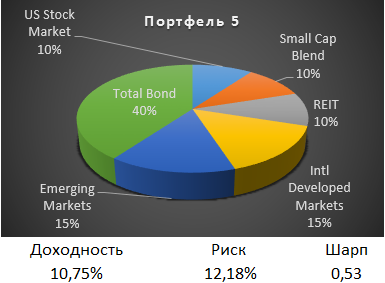
Снизим долю широкого индекса акций США до 10% и добавим акции малой капитализации США. В результате это увеличило доходность портфеля до 10,75%, и риск до 12,18%. А коэффициент Шарпа улучшился до 0,53.
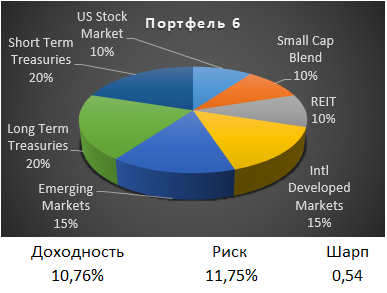
Заменим этот широкий индекс двумя другими: индексом долгосрочных облигаций и индексом краткосрочных облигаций. На профессиональном сленге это называется «гантеля».
Облигации в портфеле по прежнему занимают 40%, но теперь его доходность 10,76%, что почти так же как и у предыдущего портфеля, но зато риск ниже 11,75%. А коэффициент Шарпа вырос до 0,54.
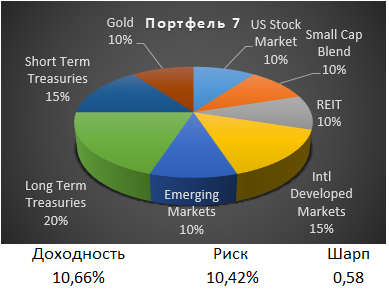
После добавления золота доходность портфеля снизилась совсем немного до 10,66%, а риск снизился заметно до 10,42%. Коэффициент Шарпа максимальный из всех рассмотренных портфелей 0,58.
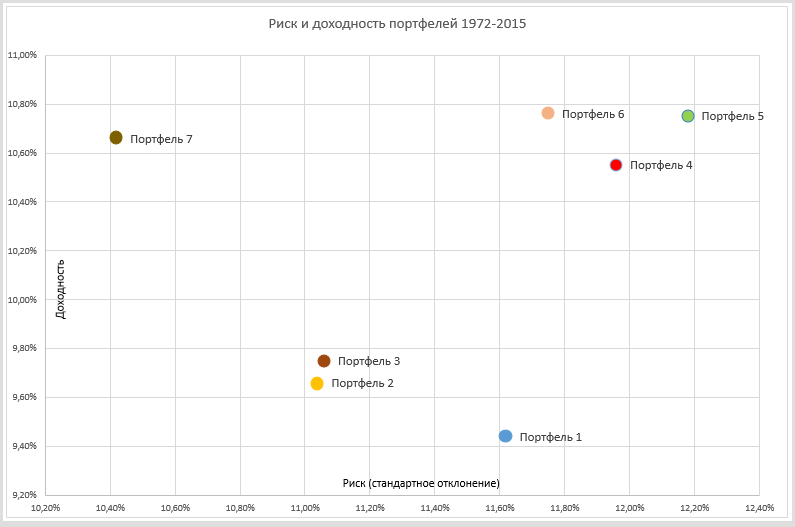
На диаграмме ниже показано расположение всех портфелей в зависимости от их риска и доходности. Можно оценить, как менялось положение того или иного портфеля, в зависимости от его состава.
Самый простой Портфель 1 имел самую низкую доходность и довольно высокий риск. Добавление недвижимости и иностранных акций (Портфель 2 и 3) снизило риск и немного увеличило доходность. Разделение иностранных акций по рынкам и добавление акций малой капитализации (Портфели 4 и 5) увеличило доходность портфеля почти на процент, но и риск тоже заметно вырос. Добавление краткосрочных и долгосрочных облигаций вместо широкого индекса (Портфель 6) немного снизило риск, почти не изменив доходность. Чтобы еще больше снизить риск, мы добавили немного золота (Портфель 7), при этом его доходность упала всего на 0,01%, а коэффициент Шарпа получился самый высокий из всех рассмотренных вариантов.
Стоит сказать, что продемонстрированные в этой статье портфели являются всего лишь примерами, а не готовыми решениями для инвестора. Какие классы активов и в какой пропорции нужно включать в портфель зависит от многих индивидуальных параметров инвестора, и с таким вопросом лучше обращаться к профессиональному финансовому консультанту.
Что такое современная теория портфеля
Поиск оптимального способа распределения активов
Хоть теория и современная, первому ее упоминанию уже 70 лет.
В основе MPT лежит тезис о том, что риск и доходность взаимосвязаны. Это означает, что желание инвестора получить более высокую доходность непременно повышает уровень риска, а между двумя портфелями с одинаковой ожидаемой доходностью рационально выбирать менее рискованный вариант.
Под риском в теории понимается волатильность портфеля — то есть то, насколько изменчива его цена. Математически волатильность выражается через статистический показатель, который называется стандартным отклонением. Пример его расчета я приводил в статье про всепогодную стратегию.
MPT утверждает, что для каждого уровня риска есть соответствующая комбинация активов, которая максимизирует доход, — такой портфель называется оптимальным. Другая идея MPT заключается в том, что за счет диверсификации по различным классам активов можно сгладить волатильность портфеля. Таким образом, мы либо максимизируем доход при заданном уровне риска, либо минимизируем риск при целевой доходности.
Рассмотрим, как это работает.
Что такое эффективная граница
На диаграмме ниже представлена так называемая эффективная граница для портфелей, составленных из акций и среднесрочных казначейских облигаций в разных пропорциях.
Оптимальные портфели расположены на фиолетовой линии. Варианты выше нее недостижимы: не существует портфелей с таким отношением доходности к риску. А портфели ниже линии неэффективны: они либо дают доходность ниже ожидаемой, либо подразумевают больший риск.
Оптимизация портфеля означает поиск компромисса между риском и прибылью. Поэтому инвестору важно заранее определиться с желаемой доходностью и комфортным для себя уровнем риска. Повторюсь, что речь здесь идет про волатильность, с которой готов мириться инвестор. Этот риск не означает полной потери актива, но может включать ее, например если компания обанкротится. Но диверсификация портфеля обычно снимает этот вопрос.
Составление инвестиционного портфеля по Марковицу для чайников
В данном обзоре мы представим простой пример составления оптимального инвестиционного портфеля по Марковицу.
Введение в портфельную теорию
Портфельная теория Марковица была обнародована в 1952 году. Позже автор получил за нее Нобелевскую премию.
Целью модели является составление оптимального портфеля, то есть с минимальным риском и максимальной доходностью.
Как правило, решается две задачи: максимизация доходности при заданном уровне риска и минимизация риска при минимально допустимом значении доходности.
Доходность портфеля измеряется как средневзвешенная сумма доходностей входящих в него бумаг.
wi — доля инструмента в портфеле;
ri — доходность инструмента.
Риск отдельного инструмента оценивается как среднеквадратичное (стандартное) отклонение его доходности. Для расчета общего риска портфеля необходимо отразить совокупное изменение рисков отдельного инструмента и их взаимное влияние (через ковариации и корреляции — меры взаимосвязи).
σi — стандартное отклонение доходностей инструмента;
kij — коэффициент корреляции между I,j-м инструментом;
Vij — ковариация доходностей i-го и j-го финансового инструмента;
n — количество финансовых инструментов в рамках портфеля.
Таким образом, в рамках правильно подобранного портфеля риски снижаются за счет обратной корреляции инструментов. При этом устраняются не только специфические риски инструмента, но и снижается систематический (рыночный) риск.
Для составления портфеля решается оптимизационная задача. При этом в базовом виде использование заемных средств не предполагается, то есть сумма долей активов равняется единице, а доли эти положительны.
Минимизируем риск при минимально допустимом уровне доходности
Максимизируем доходность при заданном уровне риска
Пример расчетов в Excel
Оптимальный портфель содержит различные группы активов — акции, облигации, товарные фьючерсы и т.д. Так легче подобрать инструменты с отрицательной корреляцией и минимизировать риски.
В нашем примере будет использован более простой подход — составление портфеля из нескольких американских акций. Для эффекта диверсификации возьмем представителей различных секторов — платежную систему VISA, ритейлера Macy’s, технологичного гиганта Apple и телеком AT&T.
Сразу отмечу, что это лишь пример. Все эмитенты интересны, но для грамотного составления портфеля необходимо учитывать фундаментальные показатели, включая рыночные мультипликаторы, оценивать технические уровни для входа в позицию.
Этап 1. Выкачиваем котировки. Необходимо взять данные минимум за год. В нашем примере были взяты ежемесячные цены закрытия с 31.06.2017 по 31.05.2018.
Этап 2. Считаем доходности по каждой бумаге. Для простоты не будем учитывать эффект дивидендов.
Считаем доходность за каждый месяц по формуле натурального логарифма. К примеру, доходность VISA за май 2018 = LN(C14/C13)
Для расчета ожидаемой доходности берем среднее значение за рассматриваемый период. В нашем случае это год. Ожидаемая доходность VISA = СРЗНАЧ(G3:G14)
Получаем отрицательную доходность AT&T, и убираем бумагу из портфеля. Сразу отмечу, что в этом заключается недостаток модели, ведь просевшие ранее акции в перспективе могут развернуться.
Этап 3. Расчет риска каждой акции. Производится по формуле стандартного отклонения. К примеру, риск VISA =СТАНДОТКЛОН(G3:G14)
Указываем окне входной интервал — ежемесячные доходности акций, а в опции «Группирование» выбираем «по столбцам».
В результате получаем ковариационную матрицу.
Этап 5. Расчет общей доходности портфеля. Для начала установим произвольные доли бумаг в портфеле. Они положительны, их сумма равна 1.
Считаем средневзвешенное значение доходностей отдельных акций. Воспользуемся формулой G15*G23+H15*H23+I15*I23
Этап 6. Расчет общего риска портфеля. Производится по формуле массива КОРЕНЬ(МУМНОЖ(МУМНОЖ(G23:I23;G20:I22); E20:E22))
Этап 7. Портфель минимального риска.
Речь идет о долях отдельных бумаг в портфеле. Для начала необходимо определить минимальный уровень допустимой доходности портфеля (rp). Возьмем rp >= 3,2%.
При оценке долей акций воспользуемся надстройкой в Excel «Поиск решений», для этого выбираем Главное меню → «Данные» → «Поиск решений».
В надстройке «Поиск решений» необходимо ввести ссылку на ячейку, которую следует оптимизировать (общий риск портфеля, минимизируем), ввести какие параметры необходимо изменять (доли акций) и ограничения. Введем ограничения на весовые значения коэффициентов у акций: сумма долей акций должна быть равна 1 и сами доли должны иметь положительный знак.
В результате имеем портфель с 73% долей VISA и 27% долей Macy’s.
Визуально портфель выглядит так:
Этап 8. Портфель максимальной доходности.
Для начала необходимо определить максимальный уровень допустимого риска портфеля (σp). Возьмем σp 30
Последние новости
Рекомендованные новости
Ход торгов. Не все голубые фишки ушли в минус
Заметные и влиятельные на фондовом рынке. Персоны года 2021
Рекорды фондового рынка 2021
Дивидендный портфель США 2022
Дивидендный портфель 2022
Инвестиции 2022: что купить. Полное руководство с прогнозами
Они вне конкуренции. Компании США и России с самой широкой маржой
Ключевые риски 2022
Адрес для вопросов и предложений по сайту: bcs-express@bcs.ru
* Материалы, представленные в данном разделе, не являются индивидуальными инвестиционными рекомендациями. Финансовые инструменты либо операции, упомянутые в данном разделе, могут не подходить Вам, не соответствовать Вашему инвестиционному профилю, финансовому положению, опыту инвестиций, знаниям, инвестиционным целям, отношению к риску и доходности. Определение соответствия финансового инструмента либо операции инвестиционным целям, инвестиционному горизонту и толерантности к риску является задачей инвестора. ООО «Компания БКС» не несет ответственности за возможные убытки инвестора в случае совершения операций, либо инвестирования в финансовые инструменты, упомянутые в данном разделе.
Информация не может рассматриваться как публичная оферта, предложение или приглашение приобрести, или продать какие-либо ценные бумаги, иные финансовые инструменты, совершить с ними сделки. Информация не может рассматриваться в качестве гарантий или обещаний в будущем доходности вложений, уровня риска, размера издержек, безубыточности инвестиций. Результат инвестирования в прошлом не определяет дохода в будущем. Не является рекламой ценных бумаг. Перед принятием инвестиционного решения Инвестору необходимо самостоятельно оценить экономические риски и выгоды, налоговые, юридические, бухгалтерские последствия заключения сделки, свою готовность и возможность принять такие риски. Клиент также несет расходы на оплату брокерских и депозитарных услуг, подачи поручений по телефону, иные расходы, подлежащие оплате клиентом. Полный список тарифов ООО «Компания БКС» приведен в приложении № 11 к Регламенту оказания услуг на рынке ценных бумаг ООО «Компания БКС». Перед совершением сделок вам также необходимо ознакомиться с: уведомлением о рисках, связанных с осуществлением операций на рынке ценных бумаг; информацией о рисках клиента, связанных с совершением сделок с неполным покрытием, возникновением непокрытых позиций, временно непокрытых позиций; заявлением, раскрывающим риски, связанные с проведением операций на рынке фьючерсных контрактов, форвардных контрактов и опционов; декларацией о рисках, связанных с приобретением иностранных ценных бумаг.
Приведенная информация и мнения составлены на основе публичных источников, которые признаны надежными, однако за достоверность предоставленной информации ООО «Компания БКС» ответственности не несёт. Приведенная информация и мнения формируются различными экспертами, в том числе независимыми, и мнение по одной и той же ситуации может кардинально различаться даже среди экспертов БКС. Принимая во внимание вышесказанное, не следует полагаться исключительно на представленные материалы в ущерб проведению независимого анализа. ООО «Компания БКС» и её аффилированные лица и сотрудники не несут ответственности за использование данной информации, за прямой или косвенный ущерб, наступивший вследствие использования данной информации, а также за ее достоверность.
Составление инвестиционного портфеля по Марковицу для чайников
В данном обзоре мы представим простой пример составления оптимального инвестиционного портфеля по Марковицу.
Введение в портфельную теорию
Портфельная теория Марковица была обнародована в 1952 году. Позже автор получил за нее Нобелевскую премию.
Целью модели является составление оптимального портфеля, то есть с минимальным риском и максимальной доходностью.
Как правило, решается две задачи: максимизация доходности при заданном уровне риска и минимизация риска при минимально допустимом значении доходности.
Доходность портфеля измеряется как средневзвешенная сумма доходностей входящих в него бумаг.
wi — доля инструмента в портфеле;
ri — доходность инструмента.
Риск отдельного инструмента оценивается как среднеквадратичное (стандартное) отклонение его доходности. Для расчета общего риска портфеля необходимо отразить совокупное изменение рисков отдельного инструмента и их взаимное влияние (через ковариации и корреляции — меры взаимосвязи).
σi — стандартное отклонение доходностей инструмента;
kij — коэффициент корреляции между I,j-м инструментом;
Vij — ковариация доходностей i-го и j-го финансового инструмента;
n — количество финансовых инструментов в рамках портфеля.
Таким образом, в рамках правильно подобранного портфеля риски снижаются за счет обратной корреляции инструментов. При этом устраняются не только специфические риски инструмента, но и снижается систематический (рыночный) риск.
Для составления портфеля решается оптимизационная задача. При этом в базовом виде использование заемных средств не предполагается, то есть сумма долей активов равняется единице, а доли эти положительны.
Минимизируем риск при минимально допустимом уровне доходности
Максимизируем доходность при заданном уровне риска
Пример расчетов в Excel
Оптимальный портфель содержит различные группы активов — акции, облигации, товарные фьючерсы и т.д. Так легче подобрать инструменты с отрицательной корреляцией и минимизировать риски.
В нашем примере будет использован более простой подход — составление портфеля из нескольких американских акций. Для эффекта диверсификации возьмем представителей различных секторов — платежную систему VISA, ритейлера Macy’s, технологичного гиганта Apple и телеком AT&T.
Сразу отмечу, что это лишь пример. Все эмитенты интересны, но для грамотного составления портфеля необходимо учитывать фундаментальные показатели, включая рыночные мультипликаторы, оценивать технические уровни для входа в позицию.
Этап 1. Выкачиваем котировки. Необходимо взять данные минимум за год. В нашем примере были взяты ежемесячные цены закрытия с 31.06.2017 по 31.05.2018.
Этап 2. Считаем доходности по каждой бумаге. Для простоты не будем учитывать эффект дивидендов.
Считаем доходность за каждый месяц по формуле натурального логарифма. К примеру, доходность VISA за май 2018 = LN(C14/C13)
Для расчета ожидаемой доходности берем среднее значение за рассматриваемый период. В нашем случае это год. Ожидаемая доходность VISA = СРЗНАЧ(G3:G14)
Получаем отрицательную доходность AT&T, и убираем бумагу из портфеля. Сразу отмечу, что в этом заключается недостаток модели, ведь просевшие ранее акции в перспективе могут развернуться.
Этап 3. Расчет риска каждой акции. Производится по формуле стандартного отклонения. К примеру, риск VISA =СТАНДОТКЛОН(G3:G14)
Указываем окне входной интервал — ежемесячные доходности акций, а в опции «Группирование» выбираем «по столбцам».
В результате получаем ковариационную матрицу.
Этап 5. Расчет общей доходности портфеля. Для начала установим произвольные доли бумаг в портфеле. Они положительны, их сумма равна 1.
Считаем средневзвешенное значение доходностей отдельных акций. Воспользуемся формулой G15*G23+H15*H23+I15*I23
Этап 6. Расчет общего риска портфеля. Производится по формуле массива КОРЕНЬ(МУМНОЖ(МУМНОЖ(G23:I23;G20:I22); E20:E22))
Этап 7. Портфель минимального риска.
Речь идет о долях отдельных бумаг в портфеле. Для начала необходимо определить минимальный уровень допустимой доходности портфеля (rp). Возьмем rp >= 3,2%.
При оценке долей акций воспользуемся надстройкой в Excel «Поиск решений», для этого выбираем Главное меню → «Данные» → «Поиск решений».
В надстройке «Поиск решений» необходимо ввести ссылку на ячейку, которую следует оптимизировать (общий риск портфеля, минимизируем), ввести какие параметры необходимо изменять (доли акций) и ограничения. Введем ограничения на весовые значения коэффициентов у акций: сумма долей акций должна быть равна 1 и сами доли должны иметь положительный знак.
В результате имеем портфель с 73% долей VISA и 27% долей Macy’s.
Визуально портфель выглядит так:
Этап 8. Портфель максимальной доходности.
Для начала необходимо определить максимальный уровень допустимого риска портфеля (σp). Возьмем σp 30
Последние новости
Рекомендованные новости
Ход торгов. Не все голубые фишки ушли в минус
Заметные и влиятельные на фондовом рынке. Персоны года 2021
Рекорды фондового рынка 2021
Дивидендный портфель США 2022
Дивидендный портфель 2022
Инвестиции 2022: что купить. Полное руководство с прогнозами
Они вне конкуренции. Компании США и России с самой широкой маржой
Ключевые риски 2022
Адрес для вопросов и предложений по сайту: bcs-express@bcs.ru
* Материалы, представленные в данном разделе, не являются индивидуальными инвестиционными рекомендациями. Финансовые инструменты либо операции, упомянутые в данном разделе, могут не подходить Вам, не соответствовать Вашему инвестиционному профилю, финансовому положению, опыту инвестиций, знаниям, инвестиционным целям, отношению к риску и доходности. Определение соответствия финансового инструмента либо операции инвестиционным целям, инвестиционному горизонту и толерантности к риску является задачей инвестора. ООО «Компания БКС» не несет ответственности за возможные убытки инвестора в случае совершения операций, либо инвестирования в финансовые инструменты, упомянутые в данном разделе.
Информация не может рассматриваться как публичная оферта, предложение или приглашение приобрести, или продать какие-либо ценные бумаги, иные финансовые инструменты, совершить с ними сделки. Информация не может рассматриваться в качестве гарантий или обещаний в будущем доходности вложений, уровня риска, размера издержек, безубыточности инвестиций. Результат инвестирования в прошлом не определяет дохода в будущем. Не является рекламой ценных бумаг. Перед принятием инвестиционного решения Инвестору необходимо самостоятельно оценить экономические риски и выгоды, налоговые, юридические, бухгалтерские последствия заключения сделки, свою готовность и возможность принять такие риски. Клиент также несет расходы на оплату брокерских и депозитарных услуг, подачи поручений по телефону, иные расходы, подлежащие оплате клиентом. Полный список тарифов ООО «Компания БКС» приведен в приложении № 11 к Регламенту оказания услуг на рынке ценных бумаг ООО «Компания БКС». Перед совершением сделок вам также необходимо ознакомиться с: уведомлением о рисках, связанных с осуществлением операций на рынке ценных бумаг; информацией о рисках клиента, связанных с совершением сделок с неполным покрытием, возникновением непокрытых позиций, временно непокрытых позиций; заявлением, раскрывающим риски, связанные с проведением операций на рынке фьючерсных контрактов, форвардных контрактов и опционов; декларацией о рисках, связанных с приобретением иностранных ценных бумаг.
Приведенная информация и мнения составлены на основе публичных источников, которые признаны надежными, однако за достоверность предоставленной информации ООО «Компания БКС» ответственности не несёт. Приведенная информация и мнения формируются различными экспертами, в том числе независимыми, и мнение по одной и той же ситуации может кардинально различаться даже среди экспертов БКС. Принимая во внимание вышесказанное, не следует полагаться исключительно на представленные материалы в ущерб проведению независимого анализа. ООО «Компания БКС» и её аффилированные лица и сотрудники не несут ответственности за использование данной информации, за прямой или косвенный ущерб, наступивший вследствие использования данной информации, а также за ее достоверность.