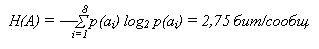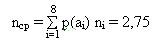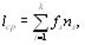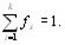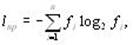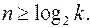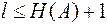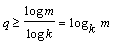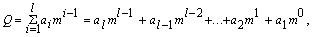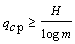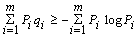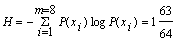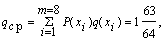За счет чего при эффективном кодировании уменьшается средняя длина кодовой комбинации
Эффективное кодирование
Как известно, большинство сообщений, формируемых источником, содержат избыточность. Удаление или уменьшение избыточности является одной из задач кодирования.
Кодирование, которое осуществляет удаление или уменьшение избыточности из закодированных сообщений, называется эффективным.
Возможность эффективного кодирования основана на теореме Шеннона, согласно которой:
Минимальное среднее количество элементов на выходе кодирующего устройства, соответствующее одному символу дискретного сообщения, можно сделать сколь угодно близким к максимальной энтропии источника.
Эффективное кодирование осуществляется с применением неравномерных кодов, в которых более короткие кодовые комбинации соответствуют более вероятным символам сообщения, а более длинные — менее вероятным символам.
Основными требованиями, предъявляемыми к эффективному коду, являются:
Рассмотрим построение эффективного кода на примере кода Шеннона-Фано и кода Хаффмена.
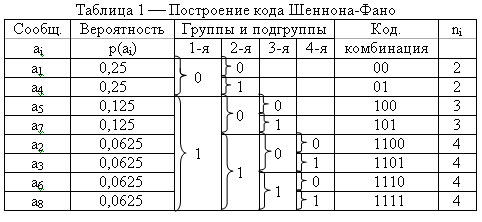
Пример 1. Источник вырабатывает восемь сообщений с вероятностями Р(а1) = Р(а4) =0,25; Р(а5) = Р(а7) = 0,125; Р(а2) = Р(а3) = Р(а6) = Р(а8) = 0,0625. Осуществить эффективное кодирование кодом Шеннона-Фано.
Для построения кода необходимо составить таблицу 1.
Заполнение таблицы осуществляется в три этапа.
1 этап. Записываются сообщения ai в порядке убывания их вероятностей (более вероятные вверху, менее вероятные внизу).
2 этап. Все сообщения делятся на две группы, таким образом, чтобы в каждой группе суммарные вероятности были примерно равны. Верхней группе присваивается ноль нижней единица. Затем каждая группа разбивается на две подгруппы, также, по возможности, с равными суммарными вероятностями. Верхней подгруппе присваивается ноль, нижней единица, и т. д. Деление подгрупп производится до тех пор, пока в каждой подгруппе не окажется по одному элементу ai.
3 этап. Записываются кодовые комбинации, соответствующие каждому элементу сообщения, при этом 1-я группа соответствует старшему разряду, 2-я следующему и т. д. по всем столбцам. Если в столбце элемента ai отсутствует символ «0» или «1», то в соответствующем разряде кодовой комбинации он не пишется.
Как видно из таблицы, каждому элементу ai соответствует своя, нигде не повторяющаяся, кодовая комбинация. Ни одна более короткая кодовая комбинация не является началом другой более длинной. При этом более вероятные символы сообщения имеют более короткие комбинации, а менее вероятные — более длинные.
Определим, удалена ли избыточность в результате кодирования.
Энтропия, приходящаяся на один символ сообщения, определяется как
Максимальная энтропия источника формирующего восемь сообщений равна
Избыточность сообщения вырабатываемого источником равна
cс = (Нmax(A) – Н(А))/Нmax(А) = (3 – 2,75)/3 = 0,09
Для определения избыточности сообщения после кодирования определим среднюю длину кодовой комбинации
Энтропия, приходящаяся на один разряд кодовой комбинации, определяется как
Нр(А) = Н(А)/nср = 2,75/2,75 = 1 бит/разряд
Максимальная энтропия на выходе двоичного дискретного источника равна
Нmax(А) = log22 = 1 бит/сообщ.
Определим коэффициент избыточности источника.
Таким образом, избыточность удалена.
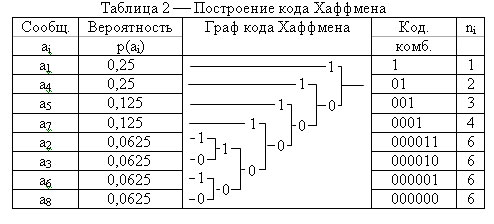
Пример 2. По приведенным в примере 1 данным необходимо осуществить эффективное кодирование кодом Хаффмена.
Построение данного кода, также удобно оформить в виде таблицы 2.
Таблица заполняется следующим образом.
1 этап. Записываются сообщения ai в порядке убывания их вероятностей (более вероятные вверху, менее вероятные внизу).
3 этап. Формируются кодовые комбинации, для этого записывают значение ветвей графа справа налево.
Эффективное кодирование



Для кодирования символов исходного алфавита используют двоичные коды переменной длины: чем больше частота символа, тем короче его код. Эффективность кодаопределяется средним числом двоичных разрядов для кодирования одного символа – lср по формуле
где k – число символов исходного алфавита;
ns – число двоичных разрядов для кодирования символа s;
fs – частота символа s; причем
где n – мощность кодируемого алфавита,
fi – частота i-го символа кодируемого алфавита.
Этот метод требует упорядочения исходного множества символов по не возрастанию их частот. Затем выполняются следующие шаги:
а) список символов делится на две части (назовем их первой и второй частями) так, чтобы суммы частот обеих частей (назовем их Σ1 и Σ2) были точно или примерно равны. В случае, когда точного равенства достичь не удается, разница между суммами должна быть минимальна;
б) кодовым комбинациям первой части дописывается 1, кодовым комбинациям второй части дописывается 0;
в) анализируют первую часть: если она содержит только один символ, работа с ней заканчивается, – считается, что код для ее символов построен, и выполняется переход к шагу г) для построения кода второй части. Если символов больше одного, переходят к шагу а) и процедура повторяется с первой частью как с самостоятельным упорядоченным списком;
г) анализируют вторую часть: если она содержит только один символ, работа с ней заканчивается и выполняется обращение к оставшемуся списку (шаг д). Если символов больше одного, переходят к шагу а) и процедура повторяется со второй частью как с самостоятельным списком;
д) анализируется оставшийся список: если он пуст – код построен, работа заканчивается. Если нет, – выполняется шаг а).
Пример 1. Даны символы a, b, c, d с частотами fa = 0,5; fb = 0,25; fc = 0,125; fd = 0,125. Построить эффективный код методом Шеннона-Фано.
Сведем исходные данные в таблицу, упорядочив их по невозрастанию частот:
| Исходные символы | Частоты символов |
| a | 0,5 |
| b | 0,25 |
| c | 0,125 |
| d | 0,125 |
Первая линия деления проходит под символом a: соответствующие суммы Σ1 и Σ2 равны между собой и равны 0,5. Тогда формируемым кодовым комбинациям дописывается 1 для верхней (первой) части и 0 для нижней (второй) части. Поскольку это первый шаг формирования кода, двоичные цифры не дописываются, а только начинают формировать код:
| Исходные символы | Частоты символов | Формируемый код |
| a | 0,5 | |
| b | 0,25 | |
| c | 0,125 | |
| d | 0,125 |
В силу того, что верхняя часть списка содержит только один элемент (символ а), работа с ней заканчивается, а эффективный код для этого символа считается сформированным (в таблице, приведенной выше, эта часть списка частот символов выделена заливкой).
Второе деление выполняется под символом b: суммы частот Σ1 и Σ2 вновь равны между собой и равны 0,25. Тогда кодовой комбинации символов верхней части дописывается 1, а нижней части – 0. Таким образом, к полученным на первом шаге фрагментам кода, равным 0, добавляются новые символы:
| Исходные символы | Частоты символов | Формируемый код |
| a | 0,5 | |
| b | 0,25 | |
| c | 0,125 | |
| d | 0,125 |
Поскольку верхняя часть нового списка содержит только один символ (b), формирование кода для него закончено (соответствующая строка таблицы вновь выделена заливкой).
Третье деление проходит между символами c и d: к кодовой комбинации символа c приписывается 1, коду символа d приписывается 0:
| Исходные символы | Частоты символов | Формируемый код |
| a | 0,5 | |
| b | 0,25 | |
| c | 0,125 | |
| d | 0,125 |
Поскольку обе оставшиеся половины исходного списка содержат по одному элементу, работа со списком в целом заканчивается.
Таким образом, получили коды:
Определим эффективность построенного кода по формуле:
lср = 0,5*1 + 0,25*01 + 0,125*3 + 0,125*3 = 1,75.
Поскольку при кодировании четырех символов кодом постоянной длины требуется два двоичных разряда, сэкономлено 0,25 двоичного разряда в среднем на один символ.
Этот метод имеет два преимущества по сравнению с методом Шеннона-Фано: он устраняет неоднозначность кодирования, возникающую из-за примерного равенства сумм частот при разделении списка на две части (линия деления проводится неоднозначно), и имеет, в общем случае, большую эффективность кода.
Исходное множество символов упорядочивается по не возрастанию частоты и выполняются следующие шаги:
1) объединение частот:
· две последние частоты списка складываются, а соответствующие символы исключаются из списка;
· оставшийся после исключения символов список пополняется суммой частот и вновь упорядочивается;
· предыдущие шаги повторяются до тех пор, пока ни получится единица в результате суммирования и список ни уменьшится до одного символа;
2) построение кодового дерева:
· строится двоичное кодовое дерево: корнем его является вершина, полученная в результате объединения частот, равная 1; листьями – исходные вершины; остальные вершины соответствуют либо суммарным, либо исходным частотам, причем для каждой вершины левая подчиненная вершина соответствует большему слагаемому, а правая – меньшему; ребра дерева связывают вершины-суммы с вершинами-слагаемыми. Структура дерева показывает, как происходило объединение частот;
· ребра дерева кодируются: каждое левое кодируется единицей, каждое правое – нулем;
3) формирование кода: для получения кодов листьев (исходных кодируемых символов) продвигаются от корня к нужной вершине и «собирают» веса проходимых ребер.
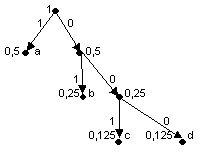
Пример 1. Даны символы a, b, c, d с частотами fa = 0,5; fb = 0,25; fc = 0,125; fd= 0,125. Построить эффективный код методом Хаффмена.
1) объединение частот (результат объединения двух последних частот в списке выделен в правом соседнем столбце заливкой):
| Исходные символы | Частоты fs | Этапы объединения | |
| первый | второй | третий | |
| a | 0,5 | 0,5 | 0,5 |
| b | 0,25 | 0,25 | 0,5 |
| c | 0,125 | 0,25 | |
| d | 0,125 |
2) построение кодового дерева:
3) формирование кода:
Как видно, полученные коды совпадают с теми, что были сформированы методом Шеннона-Фано, следовательно, они имеют одинаковую эффективность.
Основы эффективного кодирования



В технике передачи дискретных сообщений приходится решать задачу сопряжения (согласования) источников дискретных сообщений с каналом. Решение этой задачи связано с поиском путей передачи информации со скоростью, возможно более близкой к предельной.
Для большинства источников дискретных сообщений, характеризующихся информационной избыточностью, максимальная скорость передачи может быть достигнута в результате устранения избыточности в передаваемом сообщении. Процедуры, направленные на устранение избыточности источника дискретных сообщений, передаваемых по каналу без помех, называются эффективным кодированием.
Пусть имеется сообщение, записанное с помощью букв некоторого первичного алфавита 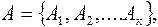
При передаче дискретных сообщений по каналам связи буквы алфавита обычно отображаются кодовыми комбинациями постоянной длины (равномерное кодирование). Длина кодовой комбинации n выбирается из условия
Применение эффективного кодирования позволяет уменьшить среднее число l двоичных символов на букву сообщения:
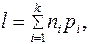
где 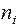
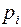
Уменьшение средней длины кодовой комбинации, отображающей букву сообщения, позволяет увечить скорость передачи.
Эффективное кодирование базируется на теореме Шеннона для каналов без шума.
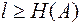
Под энтропией дискретного источника Н(А) понимается среднее количество информации, приходящееся на одну букву сообщения:
Для построения эффективных кодов наибольшее распространение нашли методики Шеннона-Фано и Хаффмена.
3.2. Метод Шеннона-Фано
1. Все К букв алфавита располагаются в один столбец в порядке убывания их вероятностей.
2. Эти буквы разбиваются на две группы: верхнюю и нижнюю так, чтобы суммы вероятностей в каждой из групп были по возможности ближе друг к другу.
4. Вновь каждую из полученных групп делят на две части с близкими, по возможности, суммарными вероятностями.
5. Верхним частям вновь образованных групп присваивается “1”, а нижним — “0”. Эти значения элементов считаются вторыми разрядами формируемых кодовых комбинаций.
Эти процедуры повторяются до тех пор, пока в каждой группе останется по одной букве.
Построение кода Шеннона-Фано для ансамбля из 8 букв приведено в
При равномерном кодировании 8-ми букв кодовые комбинации содержат по три двоичных разряда. При использовании кода Шеннона-Фано средняя длина кодовой комбинации составляет:
i=1Это меньше, чем при равномерном кодировании и не очень далеко от энтропии к
3.3. Метод Хаффмена
1. Буквы алфавита выписываются столбцом в порядке убывания вероятностей.
2. Находится сумма вероятностей последних двух букв.
3. Вероятности букв, не участвующих в объединении, и полученная суммарная вероятность снова располагаются столбцом в порядке убывания.
Второй и третий этапы повторяются до тех пор, пока суммарная вероятность не будет равна единице.
| Буквы | Рi | Деление букв на группы | Код Шеннона-Фано |
| А1 | 0,20 | ||
| А2 | 0,20 | ||
| А3 | 0,15 | ||
| А4 | 0,13 | ||
| А5 | 0,12 | ||
| А6 | 0,10 | ||
| А7 | 0,07 | ||
| А8 | 0,03 |
Построение кода Хаффмена для ансамбля из 8 букв приведено в табл. 3.2.
Таблица 3.2. Построение кода Хаффмена
| Буквы | Pi | Вспомогательные столбцы |
| 1 2 3 4 5 6 7 | ||
| А1 | 0,20 | 0,20 0,20 0,25 0,35 0,40 0,60 1 |
| А2 | 0,20 | 0,20 0,20 0,20 0,25 0,35 0,04 |
| А3 | 0,15 | 0,15 0,20 0,20 0,20 0,25 |
| А4 | 0,13 | 0,13 0,15 0,20 0,20 |
| А5 | 0,12 | 0,12 0,13 0,15 |
| А6 | 0,10 | 0,10 0,12 |
| А7 | 0,07 | 0,10 |
| А8 | 0,03 |
Кодовое дерево строится следующим образом (рис.3.1). Сначала находятся буквы с наименьшими вероятностями 0,07 (A7) и 0,03 (A8), затем от них проводятся линии к точке, изображающей “укрупненный” символ с суммарной вероятностью 0,10. На рисунке эта процедура обозначена цифрой I. Затем берутся две наименьшие вероятности со значением 0,10 и получают новый “укрупненный” символ с вероятностью 0,20 (процедура I I). Теперь наименьшие вероятности имеют символы А4 (0,13) и А5 (0,12). Соединяя их линиями формируют новый символ с суммарной вероятностью 0,25 (процедура I I I).
Эти процедуры повторяются до тех пор, пока линии от основных и “укрупненных” символов не соединятся в точке с суммарной вероятностью, равной 1. Верхнюю линию обозначают цифрой “1”, а нижнюю “0”. Любая кодовая комбинация представляет собой последовательность “1” и “0”, которые встречаются на пути от вершины дерева с вероятностью 1 к точке, изображающей нужную букву.
Сравнение рассмотренных методик построения эффективных кодов позволяет сделать вывод, что методика Хаффмена более удобна для практического использования. В общем случае код Хаффмена экономичнее кода Шеннона-Фано.
| Буква | pi | Кодовое дерево | Код | ni | nipi |
| А1 | 0,2 | 0,4 | |||
| А2 | 0,2 | 0,6 | |||
| А3 | 0,15 | 0,45 | |||
| А4 | 0,13 | 0,39 | |||
| А5 | 0,12 | 0,36 | |||
| А6 | 0,10 | 0,3 | |||
| А7 | 0,07 | 0,28 | |||
| А8 | 0,03 | 0,12 |
Рис. 3.1 Кодовое дерево.
Нетрудно заметить, что сокращение средней длины кодовой комбинации эффективного кода по сравнению с равномерными кодами достигается благодаря присвоению более вероятным буквам коротких кодовых комбинаций, а менее вероятным буквам — более длинных кодовых комбинаций. Таким образом, эффективность рассматриваемых кодов связана с различием в числе символов кодовых комбинаций. Это приводит к определенным трудностям при декодировании. Конечно, для различия кодовых комбинаций можно ставить разделительный символ, но при этом существенно снижается эффект, который достигается использованием неравномерных кодов, так как средняя длина кодовой комбинации, по существу, увеличивается на один символ. Более разумным является обеспечение однозначного декодирования без введения разделительных символов. Для этого эффективный код строят так, чтобы ни одна комбинация кода не совпадала с первыми символами более длинной кодовой комбинации. Коды, удовлетворяющие этому условию, называются префиксными.
Коды, представляющие первичные алфавиты с неравновероятными символами, имеющие минимальную среднюю длину кодового слова, называются оптимальными неравномерными кодами (ОНК).
Максимально эффективными будут те ОНК, у которых энтропия дискретного источника Н(А) численно равна среднему числу двоичных символов на букву l:
или с учетом (3.1) и (3.3)
Очевидно, что это равенство будет иметь место только тогда, когда
Величина l точно равна Н(А), если вероятности рi представляют собой целочисленные отрицательные степени двойки. Если это не выполняется, то l>Н(А) и согласно основной теореме кодирования Шеннона для каналов без шумов средняя длина кодовой комбинации приближается к энтропии источника сообщений по мере укрупнения кодируемых блоков.
Для оценки эффективности ОНК предназначены следующие характеристики.
1. Коэффициент статистического сжатия.


Он характеризует уменьшение количества двоичных символов на букву алфавита при применении ОНК по сравнению с применением методов нестатистического кодирования.
2. Коэффициент относительной эффективности.

Этот коэффициент показывает, насколько устраняется статистическая избыточность передаваемого сообщения.
Методы устранения избыточности позволяют эффективно использовать пропускную способность канала связи. Они полезны также в тех случаях, когда требуется хранить большой объем информации в различных запоминающих устройствах. Экономия в пропускной способности канала или в объеме запоминающего устройства приводит к снижению стоимости, сокращению размеров и веса аппаратуры. Рассмотренные методы кодирования получили применение при передаче факсимильных сообщений.
Эффективное кодирование
3. Эффективное кодирование
При кодировании каждая буква исходного алфавита представляется различными последовательностями, состоящими из кодовых букв (цифр).
Например, при двоичном кодировании 32 букв русского алфавита используется q = log232 = 5 разрядов, на чем и основывается телетайпный код.
Кроме двоичных кодов, наибольшее распространение получили восьмеричные коды.
Пусть, например, необходимо закодировать алфавит, состоящий из 64 букв. Для этого потребуется q = log264 = 6 двоичных разрядов или q = log864 = 2 восьмеричных разрядов. При этом буква с номером 13 при двоичном кодировании получает код 001101, а при восьмеричном кодировании 15.
Часто используются двоично-десятичные коды, в которых цифры десятичного номера буквы представляются двоичными кодами. Так, например, для рассматриваемого примера буква с номером 13 кодируется как 0001 0011. Ясно, что при различной вероятности появления букв исходного алфавита равномерный код является избыточным, т.к. его энтропия (полученная при условии, что все буквы его алфавита равновероятны): logkm = H0
всегда больше энтропии H = log m данного алфавита (полученной с учетом неравномерности появления различных букв алфавита, т.е. информационные возможности данного кода используются не полностью).
Например, для телетайпного кода Н0 = logk m = log232 = 5 бит, а с учетом неравномерности появления различных букв исходного алфавита Н » 4,35 бит. Устранение избыточности достигается применением неравномерных кодов, в которых буквы, имеющие наибольшую вероятность, кодируются наиболее короткими кодовыми последовательностями, а более длинные комбинации присваиваются редким буквам. Если i-я буква, вероятность которой Рi, получает кодовую комбинацию длины qi, то средняя длина комбинации
Считая кодовые буквы равномерными, определяем наибольшую энтропию закодированного алфавита как qср log m, которая не может быть меньше энтропии исходного алфавита Н, т.е. qср log m ³ Н.
При двоичном кодировании (m=2) приходим к соотношению qср ³ Н, или
Чем ближе значение qср к энтропии Н, тем более эффективно кодирование. В идеальном случае, когда qср » Н, код называют эффективным.
Эффективное кодирование устраняет избыточность, приводит к сокращению длины сообщений, а значит, позволяет уменьшить время передачи или объем памяти, необходимой для их хранения.
При построении неравномерных кодов необходимо обеспечить возможность их однозначной расшифровки. В равномерных кодах такая проблема не возникает, т.к. при расшифровке достаточно кодовую последовательность разделить на группы, каждая из которых состоит из q элементов. В неравномерных кодах можно использовать разделительный символ между буквами алфавита (так поступают, например, при передаче сообщений с помощью азбуки Морзе).
Если же отказаться от разделительных символов, то следует запретить такие кодовые комбинации, начальные части которых уже использованы в качестве самостоятельной комбинации. Например, если 101 означает код какой-то буквы, то нельзя использовать комбинации 1, 10 или 10101.
Практические методы оптимального кодирования просты и основаны на очевидных соображениях ( метод Шеннона – Фано ).
Пример16: Провести эффективное кодирование ансамбля из восьми знаков:
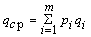
Как видно, qср = H, следовательно, полученный код является оптимальным.
Решение: При обычном (не учитывающем статистических характеристик) двоичном кодировании с использованием k=2 знаков при построении равномерного кода количество элементов в кодовой последовательности будет q ³ logk m = log2 8 = 3, т.е. для представления каждого знака использованного алфавита потребуется три двоичных символа.
Так как вероятности знаков представляют собой отрицательные целочисленные степени двойки, то избыточность при кодировании устранена полностью.
Среднее число символов на знак в этом случае точно равно энтропии. В общем случае для алфавита из восьми знаков среднее число символов на знак будет меньше трех, но больше энтропии алфавита. Вычислим энтропию алфавита:
Вычислим среднее число символов на знак:
Решение: 1. Средняя длина кодовых комбинаций