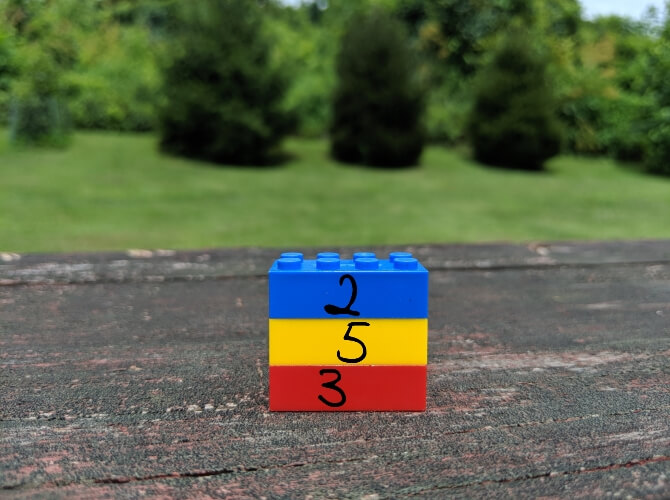За счет чего удается сжать данные без потерь когда
В каких случаях используется сжатие без потерь
Содержание урока
Вопросы и задания
Вопросы и задания
1. За счёт чего удаётся сжать данные без потерь? Когда это сделать принципиально невозможно?
2. Какие типы файлов сжимаются хорошо, а какие — плохо? Почему?
3. Текстовый файл, записанный в однобайтной кодировке, содержит только 33 заглавные русские буквы, цифры и пробел. Ответьте на следующие вопросы:
• какое минимальное число битов нужно выделить на символ при передаче, если каждый символ кодируется одинаковым числом битов?
• сколько при этом будет занимать заголовок пакета данных?
• при какой минимальной длине текста коэффициент сжатия будет больше 1?
4. На чём основан алгоритм сжатия RLE? Когда он работает хорошо? Когда нет смысла его использовать?
5. Что такое префиксный код?
6. В каких случаях допустимо сжатие с потерями?
7. Опишите простейшие методы сжатия рисунков с потерями. Приведите примеры.
8. На чём основан алгоритм JPEG? Почему это алгоритм сжатия с потерями?
9. Что такое артефакты?
10. Для каких типов изображений эффективно сжатие JPEG? Когда его не стоит применять?
11. На чём основано сжатие звука в алгоритме MP3?
12. Что такое битрейт? Как он связан с качеством звука?
13. Какое качество звука принимается за эталон качества на непрофессиональном уровне?
14. Какие методы используются для сжатия видео?
Подготовьте сообщение
а) «Программы для сжатия данных»
б) «Алгоритмы сжатия изображений»
в) «Аудиокодеки»
г) «Видеокодеки»
Следующая страница 
Cкачать материалы урока
Сжатие данных без потерь (англ. lossless data compression ) — класс алгоритмов сжатия данных (видео, аудио, графики, документов, представленных в цифровом виде), при использовании которых закодированные данные однозначно могут быть восстановлены с точностью до бита, пикселя, вокселя и т.д. При этом оригинальные данные полностью восстанавливаются из сжатого состояния. Этот тип сжатия принципиально отличается от сжатия данных с потерями. Для каждого из типов цифровой информации, как правило, существуют свои оптимальные алгоритмы сжатия без потерь.
Сжатие данных без потерь используется во многих приложениях. Например, оно используется во всех файловых архиваторах. Оно также используется как компонент в сжатии с потерями.
Сжатие без потерь используется, когда важна идентичность сжатых данных оригиналу. Обычный пример — исполняемые файлы и исходный код. Некоторые графические файловые форматы (например PNG) используют только сжатие без потерь, тогда как другие (TIFF, FLIF или GIF) могут использовать сжатие как с потерями, так и без потерь.
Содержание
Сжатие и комбинаторика [ править | править код ]
Легко доказывается теорема.
Для любого N > 0 нет алгоритма сжатия без потерь, который:
Доказательство. Не ограничивая общности, можно предположить, что уменьшился файл A длины ровно N. Обозначим алфавит как Σ 



Впрочем, данная теорема нисколько не бросает тень на сжатие без потерь. Дело в том, что любой алгоритм сжатия можно модифицировать так, чтобы он увеличивал размер не более чем на 1 бит: если алгоритм уменьшил файл, пишем «1», потом сжатую последовательность, если увеличил — пишем «0», затем исходную.
Так что несжимаемые фрагменты не приведут к бесконтрольному «раздуванию» архива. «Реальных» же файлов длины N намного меньше, чем 256 N > 
Метод сжатия без потерь [ править | править код ]
В общих чертах смысл сжатия без потерь таков: в исходных данных находят какую-либо закономерность и с учётом этой закономерности генерируют вторую последовательность, которая полностью описывает исходную. Например, для кодирования двоичных последовательностей, в которых много нулей и мало единиц, мы можем использовать такую замену:
В таком случае шестнадцать битов
будут преобразованы в тринадцать битов
Такая подстановка является префиксным кодом, то есть обладает такой особенностью: если мы запишем сжатую строку без пробелов, мы всё равно сможем расставить в ней пробелы — а значит, восстановить исходную последовательность. Наиболее известным префиксным кодом является код Хаффмана.
Большинство алгоритмов сжатия без потерь работают в две стадии: на первой генерируется статистическая модель для входящих данных, вторая отображает входящие данные в битовом представлении, используя модель для получения «вероятностных» (то есть часто встречаемых) данных, которые используются чаще, чем «невероятностные».
Статистические модели алгоритмов для текста (или текстовых бинарных данных, таких как исполняемые файлы) включают:
Алгоритмы кодирования через генерирование битовых последовательностей:
Сжатие информации
Кодирование делится на три большие группы – сжатие (эффективные коды), помехоустойчивое кодирование и криптография.
Коды, предназначенные для сжатия информации, делятся, в свою очередь, на коды без потерь и коды с потерями.
Кодирование без потерь подразумевает абсолютно точное восстановление данных после декодирования и может применяться для сжатия любой информации.
Кодирование с потерями имеет обычно гораздо более высокую степень сжатия, чем кодирование без потерь, но допускает некоторые отклонения декодированных данных от исходных.
Сжатие с потерями применяется в основном для графики (JPEG), звука (MP3), видео (MPEG), то есть там, где мелкие отклонения от оригинала незаметны или несущественны, а степень сжатия в силу огромных размеров файлов очень важна.
Сжатие без потерь применяется во всех остальных случаях – для текстов, исполняемых файлов, высококачественного звука и графики и т.д. и т.п.
Сжатие необходимо для сокращения длины сообщения и уменьшения времени для его передачи по каналам связи. Все используемые методы упаковки информации можно разделить на два класса: упаковка без потери информации и упаковка с потерей информации.
Сжатие представляет собой предмет выбора оптимального решения. Более эффективный алгоритм требует больше процессорной мощности или времени, необходимого для декодирования информации.
Один из самых простых способов сжатия информации – групповое кодирование. В соответствии с этой схемой серии повторяющихся величин (например, число) заменяются единственной величиной и количеством. Например, аbbbbccdddeeee заменяется на 1a4b2c3d4e. Формат графических файлов PCX использует этот метод.
Простейшие алгоритмы сжатия, называемые также алгоритмами оптимального кодирования, основаны на учете распределения вероятностей элементов исходного сообщения (текста, изображения, файла). На практике обычно в качестве приближения к вероятностям используют частоты встречаемости элементов в исходном сообщении. Вероятность — абстрактное математическое понятие, связанное с бесконечными экспериментальными выборками данных, а частота встречаемости — величина, которую можно вычислить для конечных множеств данных. При достаточно большом количестве элементов в множестве экспериментальных данных можно говорить, что частота встречаемости элемента близка (с некоторой точностью) к его вероятности.
Если вероятности неодинаковы, то имеется возможность наиболее вероятным (часто встречающимся) элементам сопоставить более короткие кодовые слова и, наоборот, маловероятным элементам сопоставить более длинные кодовые слова. Таким способом можно уменьшить среднюю длину кодового слова. Оптимальный алгоритм кодирования делает это так, чтобы средняя длина кодового слова была минимальной, т. е. при меньшей длине кодирование станет необратимым. Такой алгоритм существует, он был разработан Хаффманом и носит его имя. Этот алгоритм используется, например, при создании файлов в формате JPEG.
Методом Хаффмана представляет общую схему сжатия, которая имеет много вариантов. Основная схема – присвоение двоичного кода каждой уникальной величине, причем длина этих кодов различна.
Для того чтобы сформировать минимальный код для каждого символа сообщения, используется двоичное дерево. В основном алгоритме метода объединяются вместе элементы, повторяющиеся наименее часто, затем пара рассматривается как один элемент и их частоты объединяются. Это повторяется до тех пор, пока все элементы не объединятся в пары.
Рассмотрим пример. Пусть дано сообщение abbbcccddeeeeeeeeef.
Частоты символов: а: 1, b: 3, c: 3, d: 2, e: 9, f: 1.

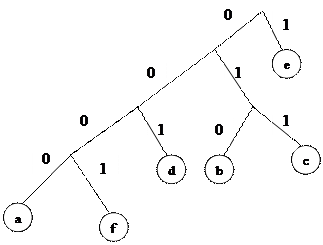 |
Частоты первых двух символов (a и f) суммируются, что дает 2. Поскольку теперь самая низкая частота 2, эта пара объединяется с d (тоже имеет частоту – 2). Исходной паре присваивается нулевая ветвь, а d – первая. Теперь код для a заканчивается на 00, f – на 01, d – на 1. Код для d будет короче на 1 бит. Дерево строится подобным образом для всех символов. Получаем следующие коды:
Исходная последовательность будет закодирована следующим образом: 00000100100100110110110010011111111110001.
Полученная таблица кодов передается приемнику информации и используется при декодировании. По алгоритму Хаффмана наименее распространенные символы кодируются более длинным кодом, наиболее распространенные – коротким.
В результате может быть получена степень сжатия 8:1, что зависит от исходного формата представления информации (1 байт на 1 символ, например, или 2 байта).
Схема Хаффмана работает не так хорошо для информации, содержащей длинные последовательности повторяющихся символов, которые могут быть сжаты лучше с использованием групповой или какой-либо другой схемы кодирования.
Вследствие того, что алгоритм Хаффмана реализуется в два прохода (1 – накопление статистики при построении статистической модели, 2 – кодирование), компрессия и декомпрессия в данном алгоритме – сравнительно медленные процессы.
Другая проблема заключается в чувствительности к отброшенным или добавленным битам. Поскольку все биты сжимаются без учета границ байта, единственный способ, при помощи которого дешифратор может узнать о завершении кода, – достигнуть конца ветви. Если бит отброшен или добавлен, дешифратор начинает обработку с середины кода, и остальная часть данных становится бессмыслицей.Полученная таблица кодов передается приемнику информации и используется при декодировании. По алгоритму Хаффмана наименее распространенные символы кодируются более длинным кодом, наиболее распространенные – коротким.
В результате может быть получена степень сжатия 8:1, что зависит от исходного формата представления информации (1 байт на 1 символ, например, или 2 байта).
Схема Хаффмана работает не так хорошо для информации, содержащей длинные последовательности повторяющихся символов, которые могут быть сжаты лучше с использованием групповой или какой-либо другой схемы кодирования.
Вследствие того, что алгоритм Хаффмана реализуется в два прохода (1 – накопление статистики при построении статистической модели, 2 – кодирование), компрессия и декомпрессия в данном алгоритме – сравнительно медленные процессы.
Другая проблема заключается в чувствительности к отброшенным или добавленным битам. Поскольку все биты сжимаются без учета границ байта, единственный способ, при помощи которого дешифратор может узнать о завершении кода, – достигнуть конца ветви. Если бит отброшен или добавлен, дешифратор начинает обработку с середины кода, и остальная часть данных становится бессмыслицей.
| | | следующая лекция ==> | |
| Параметры семплирования | | | Информационные революции |
Дата добавления: 2014-01-06 ; Просмотров: 372 ; Нарушение авторских прав? ;
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Простым языком о том, как работает сжатие файлов
Сжатие файлов позволяет быстрее передавать, получать и хранить большие файлы. Оно используется повсеместно и наверняка хорошая вам знакомо: самые популярные расширения сжатых файлов — ZIP, JPEG и MP3. В этой статье кратко рассмотрим основные виды сжатия файлов и принципы их работы.
Что такое сжатие?
Сжатие файла — это уменьшение его размера при сохранении исходных данных. В этом случае файл занимает меньше места на устройстве, что также облегчает его хранение и передачу через интернет или другим способом. Важно отметить, что сжатие не безгранично и обычно делится на два основных типа: с потерями и без потерь. Рассмотрим каждый из них по отдельности.
Сжатие с потерями
Такой способ уменьшает размер файла, удаляя ненужные биты информации. Чаще всего встречается в форматах изображений, видео и аудио, где нет необходимости в идеальном представлении исходного медиа. MP3 и JPEG — два популярных примера. Но сжатие с потерями не совсем подходит для файлов, где важна вся информация. Например, в текстовом файле или электронной таблице оно приведёт к искажённому выводу.
MP3 содержит не всю аудиоинформацию из оригинальной записи. Этот формат исключает некоторые звуки, которые люди не слышат. Вы заметите, что они пропали, только на профессиональном оборудовании с очень высоким качеством звука, поэтому для обычного использования удаление этой информации позволит уменьшить размер файла практически без недостатков.
Аналогично файлы JPEG удаляют некритичные части изображений. Например, в изображении с голубым небом сжатие JPEG может изменить все пиксели на один или два оттенка синего вместо десятков.
Чем сильнее вы сжимаете файл, тем заметнее становится снижение качества. Вы, вероятно, замечали такое, слушая некачественную музыку в формате MP3, загруженную на YouTube. Например, сравните музыкальный трек высокого качества с сильно сжатой версией той же песни.
Сжатие с потерями подходит, когда файл содержит больше информации, чем нужно для ваших целей. Например, у вас есть огромный файл с исходным (RAW) изображением. Целесообразно сохранить это качество для печати изображения на большом баннере, но загружать исходный файл в Facebook будет бессмысленно. Картинка содержит множество данных, не заметных при просмотре в социальных сетях. Сжатие картинки в высококачественный JPEG исключает некоторую информацию, но изображение выглядит почти как оригинал.
При сохранении в формате с потерями, вы зачастую можете установить уровень качества. Например, у многих графических редакторов есть ползунок для выбора качества JPEG от 0 до 100. Экономия на уровне 90 или 80 процентов приводит к небольшому уменьшению размера файла с незначительной визуальной разницей. Но сохранение в плохом качестве или повторное сохранение одного и того же файла в формате с потерями ухудшит его.
Посмотрите на этот пример.
Оригинальное изображение, загруженное с Pixabay в формате JPEG. 874 КБ:
Результат сохранения в формате JPEG с 50-процентным качеством. Выглядит не так уж плохо. Вы можете заметить артефакты по краям коробок только при увеличении. 310 КБ:
Исходное изображение, сохранённое в формате JPEG с 10-процентным качеством. Выглядит ужасно. 100 КБ:
Где используется сжатие с потерями
Как мы уже упоминали, сжатие с потерями отлично подходит для большинства медиафайлов. Это крайне важно для таких компаний как Spotify и Netflix, которые постоянно транслируют большие объёмы информации. Максимальное уменьшение размера файла при сохранении качества делает их работу более эффективной.
Сжатие без потерь
Сжатие без потерь позволяет уменьшить размер файла так, чтобы в дальнейшем можно было восстановить первоначальное качество. В отличие от сжатия с потерями, этот способ не удаляет никакую информацию. Рассмотрим простой пример. На картинке ниже стопка из 10 кирпичей: два синих, пять жёлтых и три красных.
Вместо того чтобы показывать все 10 блоков, мы можем удалить все кирпичи одного цвета, кроме одного. Используя цифры, чтобы показать, сколько кирпичей каждого цвета было, мы представляем те же данные используя гораздо меньше кирпичей — три вместо десяти.
Это простая иллюстрация того, как осуществить сжатие без потерь. Та же информация сохраняется более эффективным способом. Рассмотрим реальный файл: mmmmmuuuuuuuoooooooooooo. Его можно сжать до гораздо более короткой формы: m5u7o12. Это позволяет использовать 7 символов вместо 24 для представления одних и тех же данных.
Где используется сжатие без потерь
ZIP-файлы — популярный пример сжатия без потерь. Хранить информацию в виде ZIP-файлов более эффективно, при этом когда вы распаковываете архив, там присутствует вся оригинальная информация. Это актуально для исполняемых файлов, так как после сжатия с потерями распакованная версия будет повреждена и непригодна для использования.
Другие распространённые форматы без потерь — PNG для изображений и FLAC для аудио. Форматы видео без потерь встречаются редко, потому что они занимают много места.
Сжатие с потерями vs сжатие без потерь
Теперь, когда мы рассмотрели обе формы сжатия файлов, может возникнуть вопрос, когда и какую следует использовать. Здесь всё зависит от того, для чего вы используете файлы.
Скажем, вы только что откопали свою старую коллекцию компакт-дисков и хотите оцифровать её. Когда вы копируете свои компакт-диски, имеет смысл использовать формат FLAC, формат без потерь. Это позволяет получить мастер-копию на компьютере, которая обладает тем же качеством звука, что и оригинальный компакт-диск.
Позже вы, возможно, захотите загрузить музыку на телефон или старый MP3-плеер. Здесь не так важно, чтобы музыка была в идеальном качестве, поэтому вы можете конвертировать файлы FLAC в MP3. Это даст вам аудиофайл, который по-прежнему достаточно хорош для прослушивания, но не занимает много места на мобильном устройстве. Качество MP3, преобразованного из FLAC, будет таким же, как если бы вы создали сжатый MP3 с оригинального CD.
Тип данных, представленных в файле, также может определять, какой вид сжатия подходит больше. В PNG используется сжатие без потерь, поэтому его хорошо использовать для изображений, в которых много однотонного пространства. Например, для скриншотов. Но PNG занимает гораздо больше места, когда картинка состоит из смеси множества цветов, как в случае с фотографиями. В этом случае с точки зрения размера файлов лучше использовать JPEG.
Проблемы во время сжатия файлов
Бесполезно конвертировать формат с потерями в формат без потерь. Это пустая трата пространства. Скажем, у вас есть MP3-файл весом в 3 МБ. Преобразование его в FLAC может привести к увеличению размера до 30 МБ. Но эти 30 МБ содержат только те звуки, которые имел уже сжатый MP3. Качество звука от этого не улучшится, но объём станет больше.
Также стоит иметь в виду, что преобразовывая один формат с потерями в аналогичный, вы получаете дальнейшее снижение качества. Каждый раз, когда вы применяете сжатие с потерями, вы теряете больше деталей. Это становится всё более и более заметно, пока файл по существу не будет разрушен. Помните также, что форматы с потерями удаляют некоторые данные и их невозможно восстановить.
Заключение
Мы рассмотрели как сжатие файлов с потерями, так и без потерь, чтобы увидеть, как они работают. Теперь вы знаете, как можно уменьшить размер файла и как выбрать лучший способ для этого.
Алгоритмы, которые определяют, какие данные выбрасываются в методах с потерями и как лучше хранить избыточные данные при сжатии без потерь, намного сложнее, чем описано здесь. На эту тему можно почитать больше информации здесь, если вам интересно.
Сжатие информации без потерь. Часть первая
Доброго времени суток.
Сегодня я хочу коснуться темы сжатия данных без потерь. Несмотря на то, что на хабре уже были статьи, посвященные некоторым алгоритмам, мне захотелось рассказать об этом чуть более подробно.
Я постараюсь давать как математическое описание, так и описание в обычном виде, для того, чтобы каждый мог найти для себя что-то интересное.
В этой статье я коснусь фундаментальных моментов сжатия и основных типов алгоритмов.
Сжатие. Нужно ли оно в наше время?
Разумеется, да. Конечно, все мы понимаем, что сейчас нам доступны и носители информации большого объема, и высокоскоростные каналы передачи данных. Однако, одновременно с этим растут и объемы передаваемой информации. Если несколько лет назад мы смотрели 700-мегабайтные фильмы, умещающиеся на одну болванку, то сегодня фильмы в HD-качестве могут занимать десятки гигабайт.
Конечно, пользы от сжатия всего и вся не так много. Но все же существуют ситуации, в которых сжатие крайне полезно, если не необходимо.
Конечно, можно придумать еще множество различных ситуаций, в которых сжатие окажется полезным, но нам достаточно и этих нескольких примеров.
Все методы сжатия можно разделить на две большие группы: сжатие с потерями и сжатие без потерь. Сжатие без потерь применяется в тех случаях, когда информацию нужно восстановить с точностью до бита. Такой подход является единственно возможным при сжатии, например, текстовых данных.
В некоторых случаях, однако, не требуется точного восстановления информации и допускается использовать алгоритмы, реализующие сжатие с потерями, которое, в отличие от сжатия без потерь, обычно проще реализуется и обеспечивает более высокую степень архивации.
| Сжатие с потерями |
| Лучшие степени сжатия, при сохранении «достаточно хорошего» качества данных. Применяются в основном для сжатия аналоговых данных — звука, изображений. В таких случаях распакованный файл может очень сильно отличаться от оригинала на уровне сравнения «бит в бит», но практически неотличим для человеческого уха или глаза в большинстве практических применений. |
| Сжатие без потерь |
| Данные восстанавливаются с точностью до бита, что не приводит к каким-либо потерям информации. Однако, сжатие без потерь показывает обычно худшие степени сжатия. |
Итак, перейдем к рассмотрению алгоритмов сжатия без потерь.
Универсальные методы сжатия без потерь
В общем случае можно выделить три базовых варианта, на которых строятся алгоритмы сжатия.
Первая группа методов – преобразование потока. Это предполагает описание новых поступающих несжатых данных через уже обработанные. При этом не вычисляется никаких вероятностей, кодирование символов осуществляется только на основе тех данных, которые уже были обработаны, как например в LZ – методах (названных по имени Абрахама Лемпеля и Якоба Зива). В этом случае, второе и дальнейшие вхождения некой подстроки, уже известной кодировщику, заменяются ссылками на ее первое вхождение.
Вторая группа методов – это статистические методы сжатия. В свою очередь, эти методы делятся на адаптивные (или поточные), и блочные.
В первом (адаптивном) варианте, вычисление вероятностей для новых данных происходит по данным, уже обработанным при кодировании. К этим методам относятся адаптивные варианты алгоритмов Хаффмана и Шеннона-Фано.
Во втором (блочном) случае, статистика каждого блока данных высчитывается отдельно, и добавляется к самому сжатому блоку. Сюда можно отнести статические варианты методов Хаффмана, Шеннона-Фано, и арифметического кодирования.
Третья группа методов – это так называемые методы преобразования блока. Входящие данные разбиваются на блоки, которые затем трансформируются целиком. При этом некоторые методы, особенно основанные на перестановке блоков, могут не приводить к существенному (или вообще какому-либо) уменьшению объема данных. Однако после подобной обработки, структура данных значительно улучшается, и последующее сжатие другими алгоритмами проходит более успешно и быстро.
Общие принципы, на которых основано сжатие данных
Все методы сжатия данных основаны на простом логическом принципе. Если представить, что наиболее часто встречающиеся элементы закодированы более короткими кодами, а реже встречающиеся – более длинными, то для хранения всех данных потребуется меньше места, чем если бы все элементы представлялись кодами одинаковой длины.
Точная взаимосвязь между частотами появления элементов, и оптимальными длинами кодов описана в так называемой теореме Шеннона о источнике шифрования(Shannon’s source coding theorem), которая определяет предел максимального сжатия без потерь и энтропию Шеннона.
Немного математики
Если вероятность появления элемента si равна p(si), то наиболее выгодно будет представить этот элемент — log2p(si) битами. Если при кодировании удается добиться того, что длина всех элементов будет приведена к log2p(si) битам, то и длина всей кодируемой последовательности будет минимальной для всех возможных методов кодирования. При этом, если распределение вероятностей всех элементов F =
Это значение называют энтропией распределения вероятностей F, или энтропией источника в заданный момент времени.
Однако обычно вероятность появления элемента не может быть независимой, напротив, она находится в зависимости от каких-то факторов. В этом случае, для каждого нового кодируемого элемента si распределение вероятностей F примет некоторое значение Fk, то есть для каждого элемента F= Fk и H= Hk.
Иными словами, можно сказать, что источник находится в состоянии k, которому соответствует некий набор вероятностей pk(si) для всех элементов si.
Поэтому, учитывая эту поправку, можно выразить среднюю длину кодов как 
Где Pk — вероятность нахождения источника в состоянии k.
Итак, на данном этапе мы знаем, что сжатие основано на замене часто встречающихся элементов короткими кодами, и наоборот, а так же знаем, как определить среднюю длину кодов. Но что же такое код, кодирование, и как оно происходит?
Кодирование без памяти
Коды без памяти являются простейшими кодами, на основе которых может быть осуществлено сжатие данных. В коде без памяти каждый символ в кодируемом векторе данных заменяется кодовым словом из префиксного множества двоичных последовательностей или слов.
На мой взгляд, не самое понятное определение. Рассмотрим эту тему чуть более подробно.
Пусть задан также другой алфавит
Введем еще два обозначения для множества всех непустых слов в алфавите. Пусть 

Пусть также задано отображение F, которое ставит в соответствие каждому слову A из первого алфавита некоторое слово B=F(A) из второго. Тогда слово B будет называться кодом слова A, а переход от исходного слова к его коду будет называться кодированием.
Поскольку слово может состоять и из одной буквы, то мы можем выявить соответствие букв первого алфавита и соответствующих им слов из второго:
a1 B1
a2 B2
…
an Bn
Это соответствие называют схемой, и обозначают ∑.
В этом случае слова B1, B2,…, Bn называют элементарными кодами, а вид кодирования с их помощью — алфавитным кодированием. Конечно, большинство из нас сталкивались с таким видом кодирования, пусть даже и не зная всего того, что я описал выше.
Итак, мы определились с понятиями алфавит, слово, код, и кодирование. Теперь введем понятие префикс.
Пусть слово B имеет вид B=B’B». Тогда B’ называют началом, или префиксом слова B, а B» — его концом. Это довольно простое определение, но нужно отметить, что для любого слова B, и некое пустое слово ʌ («пробел»), и само слово B, могут считаться и началами и концами.
Итак, мы подошли вплотную к пониманию определения кодов без памяти. Последнее определение, которое нам осталось понять — это префиксное множество. Схема ∑ обладает свойством префикса, если для любых 1≤i, j≤r, i≠j, слово Bi не является префиксом слова Bj.
Проще говоря, префиксное множество – это такое конечное множество, в котором ни один элемент не является префиксом (или началом) любого другого элемента. Простым примером такого множества является, например, обычный алфавит.
Одним из канонических алгоритмов, которые иллюстрируют данный метод, является алгоритм Хаффмана.
Алгоритм Хаффмана
Алгоритм Хаффмана использует частоту появления одинаковых байт во входном блоке данных, и ставит в соответствие часто встречающимся блокам цепочки бит меньшей длины, и наоборот. Этот код является минимально – избыточным кодом. Рассмотрим случай, когда, не зависимо от входного потока, алфавит выходного потока состоит из всего 2 символов – нуля и единицы.
Для лучшей иллюстрации, рассмотрим небольшой пример.
Пусть у нас есть алфавит, состоящий из всего четырех символов — < a1, a2, a3, a4>. Предположим также, что вероятности появления этих символов равны соответственно p1=0.5; p2=0.24; p3=0.15; p4=0.11 (сумма всех вероятностей, очевидно, равна единице).
Итак, построим схему для данного алфавита.
Если сделать иллюстрацию этого процесса, получится примерно следующее:

Как вы видите, при каждом объединении мы присваиваем объединяемым символам коды 0 и 1.
Таким образом, когда дерево построено, мы можем легко получить код для каждого символа. В нашем случае коды будут выглядить так:
Поскольку ни один из данных кодов не является префиксом какого-нибудь другого (то есть, мы получили пресловутое префиксное множество), мы можем однозначно определить каждый код в выходном потоке.
Итак, мы добились того, что самый частый символ кодируется самым коротким кодом, и наоборот.
Если предположить, что изначально для хранения каждого символа использовался один байт, то можно посчитать, насколько нам удалось уменьшить данные.
Пусть на входу у нас была строка из 1000 символов, в которой символ a1 встречался 500 раз, a2 — 240, a3 — 150, и a4 — 110 раз.
Изначально данная строка занимала 8000 бит. После кодирования мы получим строку длинной в ∑pili = 500 * 1 + 240 * 2 + 150 * 3 + 110 * 3 = 1760 бит. Итак, нам удалось сжать данные в 4,54 раза, потратив в среднем 1,76 бита на кодирование каждого символа потока.
Напомню, что согласно Шеннону, средняя длина кодов составляет 
Тем не менее, следует учитывать, что помимо самих данных нам необходимо хранить таблицу кодировки, что слегка увеличит итоговый размер закодированных данных. Очевидно, что в разных случаях могут с использоваться разные вариации алгоритма – к примеру, иногда эффективнее использовать заранее заданную таблицу вероятностей, а иногда – необходимо составить ее динамически, путем прохода по сжимаемым данным.
Заключение
Итак, в этой статье я постарался рассказать об общих принципах, по которым происходит сжатие без потерь, а также рассмотрел один из канонических алгоритмов — кодирование по Хаффману.
Если статья придется по вкусу хабросообществу, то я с удовольствием напишу продолжение, так как есть еще множество интересных вещей, касающихся сжатия без потерь; это как классические алгоритмы, так и предварительные преобразования данных (например, преобразование Барроуза-Уилира), ну и, конечно, специфические алгоритмы для сжатия звука, видео и изображений (самая, на мой взгляд, интересная тема).