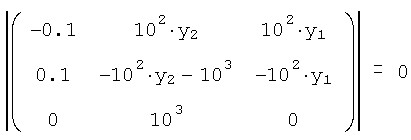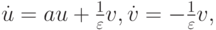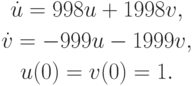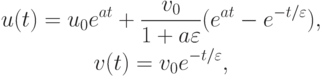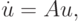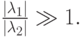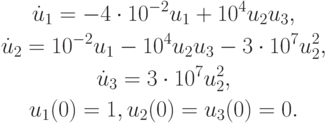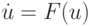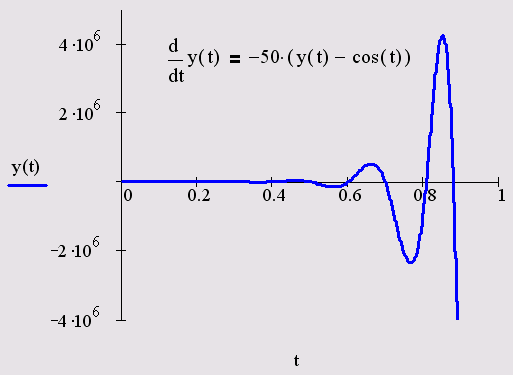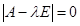Жесткие системы оду что это

Жесткие системы ОДУ

До сих пор мы имели дело с «хорошими» уравнениями, которые надежно решались численными методами (типа Рунге-Кутты). Однако имеется класс так называемых жестких (stiff) систем ОДУ, для которых стандартные методы практически неприменимы, поскольку их решение требует исключительно малого значения шага численного метода. Для этих систем разработаны специальные алгоритмы

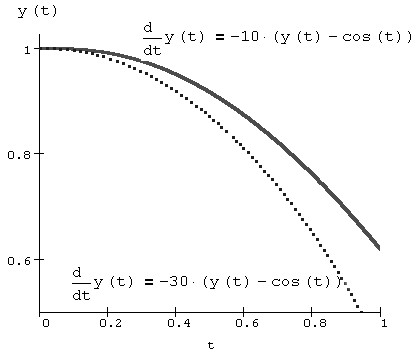
Рис. 1. Решение нежестких ОДУ методом Рунге-Кутты

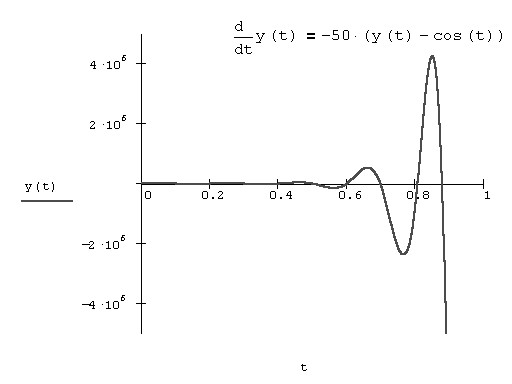
Рис. 2. Неверное решение более жесткого ОДУ методом Рунге-Кутты

Таким образом, во-первых, мы выяснили, что одни и те же уравнения (с разными параметрами) могут быть как жесткими, так и нежесткими. Во-вторых, чем жестче уравнение, тем больше шагов в обычных численных методах требуется для его устойчивого решения. С классическим примером ОДУ из листинга 11.11 все получилось хорошо, т.к. оно было не очень жестким, и небольшое увеличение числа шагов разрешило все проблемы. Для решения обычными методами более жестких уравнений требуются миллионы, миллиарды и даже большее число шагов.

Замечание Некоторые ученые замечают, что в последние годы методы Рунге-Кутты стали уступать свое главенствующее положение среди алгоритмов решения ОДУ методам, способным решать жесткие задачи.

Исторически, интерес к жестким системам возник в середине XX века при изучении уравнений химической кинетики с одновременным присутствием очень медленно и очень быстро протекающих химических реакций. Тогда неожиданно оказалось, что, как считалось, исключительно надежные методы Рунге-Кутты стали давать сбой при расчете этих задач. Рассмотрим классическую модель взаимодействия трех веществ (Робертсон, 1966), которая как нельзя лучше передает смысл понятия жесткости ОДУ.
Пусть вещество «0» медленно превращается в «1»: «0»—>»1″ (со скоростью 0.1), вещество «1» при каталитическом воздействии самого себя превращается очень быстро в вещество «2»: «1»+»1″—>»2″+»1″ (10 3 ). И, наконец подобным образом (но со средней скоростью) реагируют вещества «2» и «1»: «1»+»2″—>»0″+»2″ (10 2 ). Система ОДУ, описывающая динамику концентрации реагентов, приведена ниже.

Бросается в глаза сильно различающийся порядок коэффициентов при разных слагаемых. Именно степень этого различия чаще всего и определяет жесткость системы ОДУ. В качестве соответствующей характеристики выбирают матрицу Якоби (якобиан) векторной функции F(t,y), т.е. функциональную матрицу, составленную из производных F(t,y). Чем вырожденнее матрица Якоби, тем жестче система уравнений. В приведенном примере определитель якобиана и вовсе равен нулю при любых значениях y₀, y₁ и y₂:

Для приведенного примера стандартным методом Рунге-Кутты все-таки удается найти решение. Однако, для этого требуется очень большое число шагов, M=20000, что делает расчеты очень медленными. При меньшем числе шагов численному алгоритму не удается найти решение. Решение данной системы ОДУ приведено в разделе Модель химической кинетики главы Динамические системы.

В принципе, можно было бы снизить жесткость системы «вручную», применяя масштабирование. Для этого нужно искусственно уменьшить искомую функцию y₁, к примеру, в тысячу раз, разделив все слагаемые в системе ОДУ, содержащие y_1, на 1000. После масштабирования для решения полученной системы методом Рунге-Кутты будет достаточно взять всего M=20 шагов.

Однако, в последнее время для жестких систем ОДУ разработаны специальные, довольно эффективные алгоритмы.
Во-первых, можно использовать простые неявные алгоритмы, типа симметричной неявной схемы Эйлера, приведенной нами ранее;
Во-вторых, применяются более сложные неявные алгоритмы;
В-третьих, широко используются безытерационные алгоритмы, типа метода Розенброка.;

Источник

Лекция 10: Численные методы решения жестких систем обыкновенных дифференциальных уравнений

9.1. Явление жесткости. Предварительные сведения

Рассмотрим в качестве примера две задачи Коши для систем обыкновенных дифференциальных уравнений (ОДУ) [9.1], [9.2]:

с начальными данными u(0) = u₀, v(0) = v₀ ; здесь 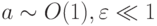; и линейную систему с постоянными коэффициентами

Решением первой задачи Коши являются функции

В обоих случаях решение состоит из двух экспонент: быстро убывающей и относительно медленно изменяющейся. Отметим, что абсолютные величины собственных значений матриц рассматриваемых линейных систем ОДУ при их представлении в виде

При моделировании физических процессов причина такой разницы в собственных числах заключена в существенно различных характерных временах процессов, описываемых системами ОДУ. Наиболее часто подобные системы встречаются при моделировании процессов в ядерных реакторах, при решении задач радиофизики, астрофизики, физики плазмы, биофизики, химической кинетики. Последние задачи часто могут быть записаны в виде [9.3]:

где u_k — концентрации веществ, участвующих в химических реакциях, скорости протекания которых характеризуются коэффициентами 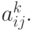В качестве примера приведем одну из систем химической кинетики, описывающую изменение концентрации трех веществ, участвующих в реакции для случая полного перемешивания [9.1].

Участки решения, характеризующиеся быстрым и медленным его изменением, называются пограничным слоем и квазистационарным режимом, соответственно.

выбирать шаг из условия

то он будет соответствовать самому быстрому процессу. В данном случае затраты машинного времени для исследования самых медленных процессов будут неоправданно велики. По этой причине имеются следующие альтернативы в выборе подхода к численному решению рассматриваемых задач.

т.е. с учетом характерных времен всех процессов, описываемых данной системой.

Источник

Что такое жесткие ОДУ?

Листании 11.11. Решение нежесткого ОДУ

Рис. 11.16. Решение нежестких ОДУ методом Рунге-Кутты (листинг 11.11)

Рис. 11.17. Неверное решение более жесткого ОДУ методом Рунге-Кутты

Таким образом, во-первых, мы выяснили, что одни и те же уравнения с разными параметрами могут быть как жесткими, так и нежесткими. Во-вторых, чем жестче уравнение, тем больше шагов в обычных численных методах требуется для его устойчивого решения. С классическим примером ОДУ из листинга 11.11 все получилось хорошо, т. к. оно было не очень жестким, и небольшое увеличение числа шагов разрешило все проблемы. Для решения обычными методами более жестких уравнений требуются миллионы, миллиарды и даже большее число шагов.

Некоторые ученые замечают, что в последние годы методы Рунге-Кутты стали уступать свое главенствующее положение среди алгоритмов решения ОДУ методам, способным решать жесткие задачи.

Исторически, интерес к жестким системам возник в середине XX века при изучении уравнений химической кинетики с одновременным присутствием очень медленно и очень быстро протекающих химических реакций. Тогда неожиданно оказалось, что считавшиеся исключительно надежными методы Рунгй-Кутты стали давать сбой при расчете этих задач. Рассмотрим классическую модель взаимодействия трех веществ (Робертсон, 1966), которая как нельзя лучше передает смысл понятия жесткости ОДУ.

Листинг 11.12. Жесткая сисема ОДУ химической кинетики

Бросается в глаза сильно различающийся порядок коэффициентов при разных слагаемых. Именно степень этого различия чаще всего и определяет жесткость системы ОДУ. В качестве соответствующей характеристики выбирают матрицу Якоби (якобиан) векторной функции Fit,у), т.е. функциональную матрицу, составленную из производных F(t,y) (см. разд. «Частные производные» гл. 7). Чем вырожденнее матрица Якоби, тем жестче система уравнений. В приведенном примере определитель якобиана и вовсе равен нулю при любых значениях у„, yi и у2 (листинг 11.13, вторая строка). В первой строке листинга 11.13 приведено напоминание способа вычисления якобиана средствами Mathcad на примере определения элементов его первой строки.

Листинг 11.13. Якобиан рассматриваемой системы ОДУ химический киметики

Для примера, приведенного в листинге 11.12, стандартным методом Вунге-Кутгы все-таки удается найти решение (оно показано на рис. 11.18). Однако для этого требуется очень большое число шагов, м=2000о, что делает (расчеты очень медленными. При меньшем числе шагов численному алгоритму не удается найти решение. В процессе работы алгоритма оно расходятся, и Mathcad вместо результата выдает ошибку о превышении предельно большого числа.

Еще один факт, на который стоит обратить внимание, — это различие в порядке величины получающегося решения. Как видно из рис. 11.18, концентрация первого реагента y1 существенно (в тысячи раз) превышает концентрацию остальных. Это свойство также очень характерно для жестких систем.

В принципе, можно было бы снизить жесткость системы «вручную», применяя масштабирование. Для этого нужно искусственно уменьшить искомую функцию yl, к примеру, в тысячу раз, разделив все слагаемые в системе ОДУ, содержащие yi, на 1000. После масштабирования для решения полученной системы методом Рунге-Кутты будет достаточно взять всего М=20 шагов.

Рис. 11.18. Решение жесткой системы ОДУ химической кинетики методом Рунге-Кутты (листинг 11.12)

Источник

Жесткие системы дифференциальных уравнений

Лекция 8. Решение систем ОДУ и двухточечных краевых задач для ОДУ

В MathCAD

1. Решение систем обыкновенных дифференциальных уравнений.

Для численного интегрирования систем ОДУ в MathCAD также имеется выбор – либо использовать вычислительный блок Given/Odesolve, либо встроенные функции rkfixed, Rkadapt и Bulstoer.

При решении систем ОДУ MathCAD требует, чтобы система ОДУ была представлена в нормальной форме (когда левые части – первые производные от соответствующих функций, а в правых частях производные отсутствуют):

где Y и Y’ – соответствующие неизвестные векторные функции переменной t, а F – вектор правых частей системы уравнений первого порядка. Именно векторное представление используется для ввода системы ОДУ в среде MathCAD.

Если в систему ОДУ входят иуравнения высших порядков, то оно тоже сводится к системе уравнений первого порядка, как было показано выше. При этом количество нулевых условий для вычислительного блока Given/Odesolve, а также размер вектора начальных условий y и размер вектора правых частей F(x,y) для встроенных функций rkfixed, Rkadapt и Bulstoer должны быть равны сумме порядков всех уравнений.

Вначале покажем решение систем ОДУ первого порядка с использованием вычислительного блока Given/Odesolve

Функция Odesolve для системы ОДУ имеет несколько иной, по сравнению с одним уравнением, синтаксис. Теперь она возвращает вектор функций, составляющих решение системы. Поэтому в качестве первого аргумента функции нужно ввести вектор, состоящий из имен функций, использованных при вводе системы. Второй и третий аргументы то же самое, что и в задаче с одним ОДУ.

Решение системы ОДУ показано на графике слева. Как известно, решения ОДУ часто удобнее изображать не в таком виде, а в фазовом пространстве, по каждой из осей которого откладываются значения каждой из найденных функций (как показано на рисунке справа). При этом аргумент входит в них лишь параметрически. В рассматриваемом случае двух ОДУ такой график – фазовый портрет системы – является кривой на фазовой плоскости. В общем случае, если система состоит из N ОДУ, то фазовое пространство является N – мерным. При N > 3 наглядность теряется, и для визуализации фазового портрета приходится строить его различные проекции.

Рассмотрим решение этой же системы ОДУ первого порядка с использованием встроенной функции rkfixed.

Полученное решение полностью соответствует вышеприведенному решению с использованием вычислительного блока Given/Odesolve. Следует отметить, что начальные условия здесь задаются в виде вектора y, а функциям x(t) и y(t) соответствуют элементы этого вектора y₁ и y₂. Вектор начальных условий y и вектор правых частей F имеют размер равный двум, т.к. система состоит из двух уравнений первого порядка. Для системы ОДУ, состоящей из двух уравнений второго порядка, размер этих векторов будет равен четырем

2. Решение жестких ОДУ и систем ОДУ.

Сложно дать математически точное определение жесткости, поскольку задачи, входящие в этот класс, весьма разнообразны. Чаще всего жесткими дифференциальными уравнениями называются уравнения, в решении которых есть плавно меняющаяся компонента, а также быстро затухающие возмущения.

Жесткие системы дифференциальных уравнений

В некоторых системах дифференциальных уравнений описанные ранее методы численного решения дают плохие результаты. А именно, для достижения заданной точности приходится выбирать очень мелкий шаг, т.е. выполнять слишком большой объем вычислений. К таким системам относятся жесткие системы дифференциальных уравнений.

Определение. Система дифференциальных уравнений (7) называется жесткой вдоль решения y = j(x), если выполняются следующие два условия:

1. собственные числа l_k матрицы имеют отрицательные действительные части при любом x;

2. число жесткости велико.

Собственными числами матрицы являются корни уравнения

Напомним, что матрица – это матрица Якоби, т.е. матрица из частных производных, элементы которой имеют вид . Перед вычислением собственных чисел в эти элементы вместо y нужно подставить y = j(x), т.е. то решение, вдоль которого исследуется система на жесткость. Полученная матрица будет зависеть только от x, и ее собственные числа тоже будут зависеть от x. Условие 2 в определении жесткой системы оставляет некоторый произвол в понимании слова «велико». Насколько велико должно быть число жесткости g, определяется в зависимости от конкретной задачи. Обычно система считается жесткой, если число жесткости порядка нескольких сотен. Если система (7) – линейная, то матрица A(x,y) зависит только от x, а если система линейная с постоянными коэффициентами, то эта матрица является постоянной, т.е. числовой (наиболее простой случай). Для линейных систем условие жесткости не зависит от рассматриваемого решения.

Вот цитата из посвященной жестким уравнениям монографии К. Деккера и Я. Вервера: «Сущность явления жесткости состоит в том, что решение, которое нужно вычислить, меняется медленно, однако существуют быстро затухающие возмущения. Наличие таких возмущений затрудняет получение медленно меняющегося решения численным способом».

Для решения жестких систем дифференциальных уравнений разработаны специальные методы. Они используют неявные схемы типа интерполяционных методов, указанных выше, и используют матрицу Якоби правых частей системы уравнений.

Возможны случаи, когда система дифференциальных уравнений является жесткой только на какой-то части решения, а на остальной части жесткой не является. В этом случае можно первую часть решения найти с помощью методов для жестких систем, а другую часть – с помощью методов, описанных выше.

Для жестких систем (stiff) не работает обычный метод Рунге-Кутта или Булирша-Штера. Наличие быстро затухающего возмущения приводит к тому, что эти численные методы дают расходящееся решение. Для жестких задач разрабатываются специальные методы. В MathCAD предусмотрены три различные функции для решения жестких задач:

— Radau – метод Radaus для жестких систем. Полностью аналогичен использованию функции odesolve с выбранным в контекстном меню методом Stiff.

— Stiffb – метод Булирша-Штера, адаптированный для жестких систем.

— Stiffr – метод Розенброка.

Постановка краевых задач для ОДУ отличается от задач Коши, рассмотренных выше, тем, что граничные условия для них ставятся не в одной начальной точке, а на обеих границах расчетного интервала. Если имеется система N ОДУ первого порядка, то часть из N условий может быть поставлена на одной границе интервала, а оставшиеся условия – на противоположной границе. В связи с тем, что условия поставлены не на одной, а на обеих границах интервала, краевые задачи нельзя решить изложенными выше методами, предназначенными для задач Коши. Для решения краевой задачи в MathCAD нет отдельной функции. Однако есть функции, позволяющие превратить краевую задачу в задачу Коши. Эти функции «угадывают» недостающие начальные условия, исходя из того, что решение должно удовлетворять заданным условиям в конечной точке интервала интегрирования. Простейшей из функций, предназначенных для приведения краевой задачи к задаче Коши, является функция sbval.

Для того, чтобы решить двухточечную краевую задачу с помощью этой функции, следует выполнить следующие действия:

1. Задайте вектор v с количеством элементов равным количеству недостающих начальных условий. Значения элементов этого вектора – это начальные приближения, исходя из которых будет происходить поиск недостающих начальных условий. На данном этапе не конкретизируется, какой из элементов вектора будет соответствовать начальному значению той или иной неизвестной функции в задаче.

2. Задайте функцию F (x,y). Эта функция уже описывалась выше. Она представляет собой вектор, каждый элемент которого – это правая часть одного из уравнений системы.

3. Задайте еще одну векторную функцию load (x,v). Это функция от скалярного аргумента x и вектора v, который имеет столько же компонент, сколько недостающих начальных условий в системе. Сам вектор load должен содержать такое же количество элементов, как и вектор F, т.е. столько, сколько должно быть начальных условий в задаче. Если начальное значение какой-либо из функций известно, то соответствующий элемент вектора load должен содержать это значение. Для функций, начальное значение которых неизвестно, соответствующий элемент вектора load должен содержать один из элементов вектора v.

4. Следует задать еще одну некоторую функцию score (x,y). Аргументы этой функции – скаляр x и вектор y, который имеет столько элементов, сколько уравнений в системе. Количество компонент вектора score должно равняться количеству граничных условий, заданных в конечной точке отрезка интегрирования. На самом деле каждая компонента этого вектора задает одно из граничных условий в конечной точке. Например, если в задаче есть граничной условие y_i(b)=c, то один из элементов вектора score должен быть функцией, которая обращается в нуль при значениях x=b и y(b)=c. Конкретный вид этой функции не играет особой роли, поэтому проще всего задавать ее в таком виде: score_k(x,y):=y_i-c. Таким же образом должны быть заданы все элементы вектора score для всех конечных условий задачи.

5. Теперь все введенные величины нужно использовать как аргументы в функции sbval. Использование этой функции выглядит следующим образом: Y:=sbval(v,a,b,F,load,score). Аргументы a и b – это начало и конец отрезка интегрирования.

6. Результатом функции sbval будет вектор, содержащий недостающие начальные значения. Их последовательность задается той последовательностью, в которой были использованы компоненты вектора v в функции load.

7. Постройте вектор начальных значений, используя известные начальные значения, а также элементы вектора Y, там, где значения были неизвестны.

8. Теперь можно решить полученную задачу как задачу Коши, с помощью, например, функции Rkadapt.

Ниже приведено решение дифференциального уравнения на отрезке [0,3] с начальным условием y(0)=1 и граничным условием y(3)=4. Недостающее начальное условие – y’(0).

Источник

Жесткая система

Смотреть что такое «Жесткая система» в других словарях:

жесткая система опоры тела — 3.30 жесткая система опоры тела (rigid body support unit): Сформованное сиденье или откинутое устройство, изготовленное из твердых материалов (при необходимости драпированных) или из эластичных материалов, помещенных в жесткий кожух, вместе со… … Словарь-справочник терминов нормативно-технической документации

мгновенно-жесткая система — Исключительный случай геометрически изменяемой системы, при котором она допускает лишь бесконечно малые перемещения. [Сборник рекомендуемых терминов. Выпуск 82. Строительная механика. Академия наук СССР. Комитет научно технической терминологии.… … Справочник технического переводчика

Система централизованного планирования и управления — ( ) — способ организации экономических отношений между людьми – как правило, при социализме Но бывают и исключения: она может при чрезвычайных обстоятельствах (например, военных) применяться и в условиях капитализма; тогда она называется… … Экономико-математический словарь

система централизованного планирования и управления — Способ организации экономических отношений между людьми – как правило, при социализме Но бывают и исключения: она может при чрезвычайных обстоятельствах (например, военных) применяться и в условиях капитализма; тогда она называется… … Справочник технического переводчика

СИСТЕМА — (от греч. целое, составленное из частей; соединение), совокупность элементов, находящихся в отношениях и связях друг с другом, которая образует определ. целостность, единство. Претерпев длит. историч. эволюцию, понятие С. с сер. 20 в.… … Философская энциклопедия

Система контроля и управления доступом — (СКУД) совокупность программно аппаратных технических средств безопасности, имеющих целью ограничение / регистрацию входа выхода объектов (людей, транспорта) на заданной территории через двери, ворота, проходные (т. н. «точки прохода») … Википедия

ЖЕСТКАЯ ДИФФЕРЕНЦИАЛЬНАЯ СИСТЕМА — система обыкновенных дифференциальных уравнений, при численном решении к рой явными методами типа Рунге Кутта или Адамса, несмотря на медленное изменение искомых переменных, шаг интегрирования обязан оставаться малым. Попытки уменьшить время… … Математическая энциклопедия

система вантовая жесткая — система вантовая жёсткая Система с предварительно напряжёнными вантами, сетками или вантовыми фермами [Терминологический словарь по строительству на 12 языках (ВНИИИС Госстроя СССР)] Тематики строительные конструкции EN rigid cable roof system DE … Справочник технического переводчика

жесткая анкерная линия — 3.3 жесткая анкерная линия (rigid anchor line): Соединительный элемент, предназначенный для подсистемы с перемещаемым средством защиты ползункового типа. Примечание Жесткой анкерной линией крепления может быть рельс или проволочный канат. Жесткая … Словарь-справочник терминов нормативно-технической документации

жесткая ссылка (на стандарты) — 94 жесткая ссылка (на стандарты): Ссылка на стандарты, определяющая один или несколько конкретных стандартов таким образом, чтобы последующие пересмотры стандарта или стандартов имели силу только после внесения изменений в регламент. Примечание… … Словарь-справочник терминов нормативно-технической документации

Источник