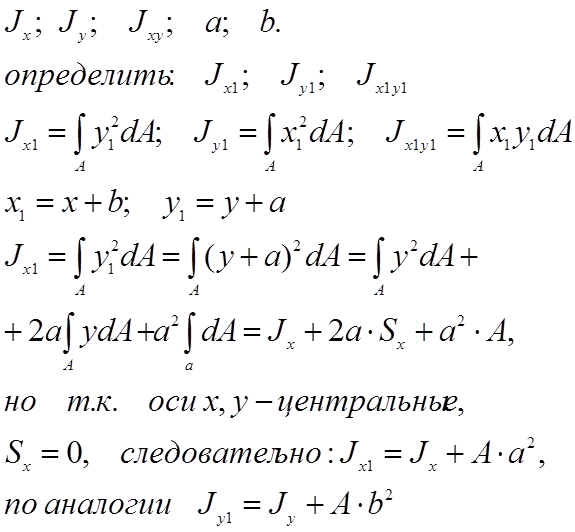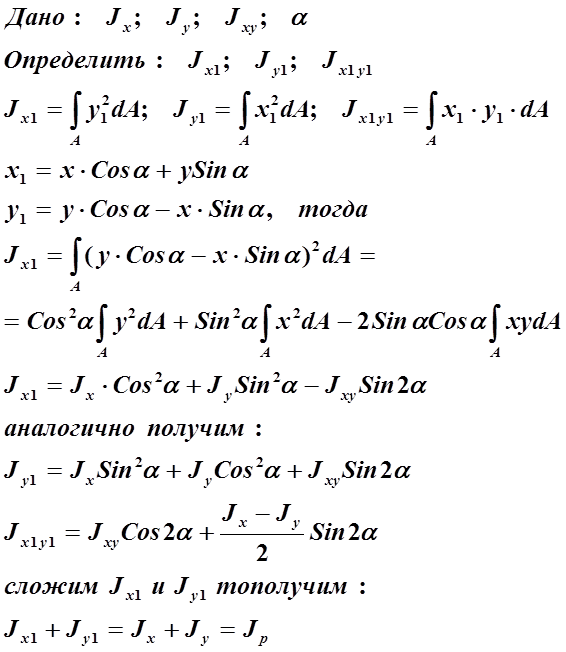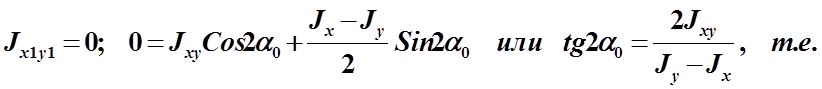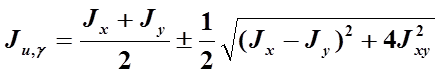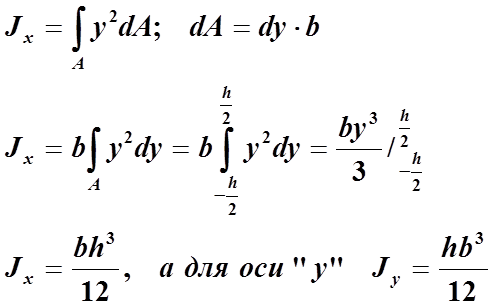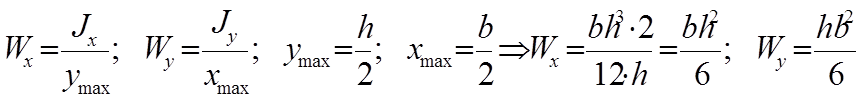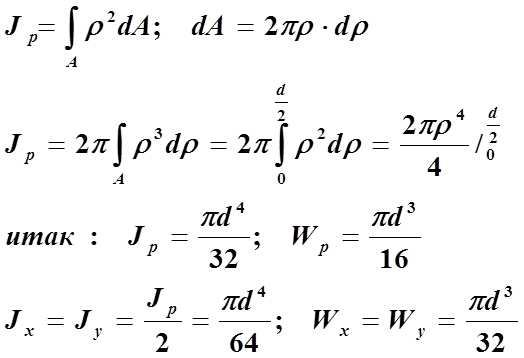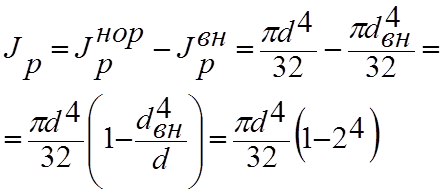Для чего необходимы геометрические характеристики плоских сечений
Геометрические характеристики плоских сечений
1.Статические моменты и моменты инерции сечения
Введем декартову прямоугольную систему координат Oxy. Рассмотрим в плоскости координат произвольное сечение (замкнутую область) с площадью A (рис. 1).
Статическими моментами сечения относительно осей x и y называются интегралы вида:
Точка C с координатами (xC, yC)
Если оси координат проходят через центр тяжести сечения, то статические моменты сечения равны нулю:
Осевыми моментами инерции сечения относительно осей x и y называются интегралы вида:
Полярным моментом инерции сечения относительно начала координат называется интеграл вида:
Центробежным моментом инерции сечения называется интеграл вида:
2.Теорема Штейнера-Гюйгенса о параллельном переносе осей
3.Изменение моментов инерции при повороте осей
Если известны моменты инерции Ix и Iy относительно осей x и y, то относительно осей ν и u, повернутых на угол α, моменты инерции осевые и центробежный вычисляют по формулам:
Из приведенных формул видно, что
где α0 – угол, на который надо развернуть оси x и y, чтобы они стали главными (положительный угол принято откладывать против хода часовой стрелки, отрицательный – по ходу часовой стрелки). Осевые моменты инерции относительно главных осей называются главными моментами инерции :
знак плюс перед вторым слагаемым относится к максимальному моменту инерции, знак минус – к минимальному.
Научная электронная библиотека
Лекция 4. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ СТЕРЖНЯ
Математические определения геометрических характеристик плоских фигур: статические моменты, осевые моменты инерции и центробежный, полярный момент инерции. Центральные оси. Главные оси. Определение положения центра тяжести элементарных сечений и составленного из элементарных фигур. Нахождение геометрических характеристик сечений относительно центральных осей.
Различают следующие характеристики сечений: площадь А, статические моменты площади, моменты инерции площади, центробежный момент инерции площади.
Рис. 10. Площадь А в системе координат х, у
Под статическим моментом площади относительно некоторой оси понимается сумма произведений площадей элементарных площадок на расстояния от их центра тяжести до соответствующей оси:
Определение центра тяжести сечения. Статические моменты сечения относительно осей проходящих через центр тяжести равны нулю, поэтому их используют для определения координат центров тяжести сечения. Для этого проводят вспомогательные оси x и y и координаты центра тяжести сечения определяют по зависимостям:
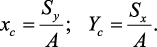
Моменты инерции сечения. Осевым моментом инерции сечения I называется интеграл по площади произведения элементарной площадки на квадрат расстояния до оси. Осевые моменты инерции сечения относительно осей x и y будут соответственно равны
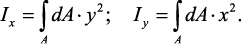
Полярным моментом инерции сечения Iρ называется интеграл по площади произведения элементарной площадки на квадрат расстояния до начало координат.
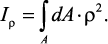
Полярный момент инерции сечения равен сумме осевых моментов инерции сечения.
Оси, относительно которых центробежный момент инерции равен нулю, называются главными центральными осями, осевые моменты инерции относительно их принимают свои экстремальные значения (максимум и минимум).
Полярный момент инерции
Полярный момент инерции относительно данной точки – сумма произведений элементарных площадей dA на квадраты их расстояний (ρ 2 = y 2 + z 2 ) до этой точки, взятая по всей площади сечения А.
Моменты сопротивления. Осевой момент сопротивления относительно рассматриваемой оси – величина равная моменту инерции относительно той же оси отнесенному к расстоянию до наиболее удаленной от этой оси точки
Полярный момент сопротивления
Осевой и полярный моменты сопротивления имеют размерность м3.
Радиус инерции
Радиусом инерции сечения относительно некоторой оси, называется величина, определяемая из соотношения:
Вычисление геометрических характеристик простых фигур.
Определим осевой момент инерции прямоугольника относительно оси х.
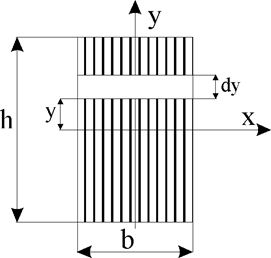
Разобьем площадь прямоугольника на элементарные площадки с размерами b (ширина) и dy (высота) (рис. 11). Тогда площадь такого элементарного прямоугольника (заштрихована)равна dA = b•dy. Подставляя значение dA в формулу для определения осевого момента инерции, получим:
По аналогии запишем
Вначале целесообразно найти полярный момент инерции. Затем, учитывая, что для круга Jx = Jy, а Jρ = Jx + Jy, найдем Jx = Jy = Jρ/2.
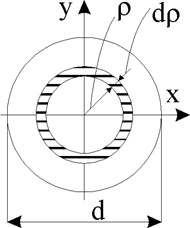
Разобьем круг на бесконечно малые кольца толщиной dρ и радиусом ρ (рис. 12); площадь такого кольца 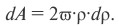
Геометрические характеристики плоских сечений
Страницы работы
Содержание работы
ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ.
Как показывает опыт, сопротивление стержня различным деформациям зависит не только от размеров поперечного сечения, но и от формы.
Размеры поперечного сечения и форма характеризуются различными геометрическими характеристиками: площадь поперечного сечения, статические моменты, моменты инерции, моменты сопротивления и др.
1. Статический момент площади (момент инерции первой степени).
Статический моментом инерции площади относительно какой-либо оси, называется сумма произведений элементарных площадок на расстояние до этой оси, распространенная на всю площадь (рис. 1)
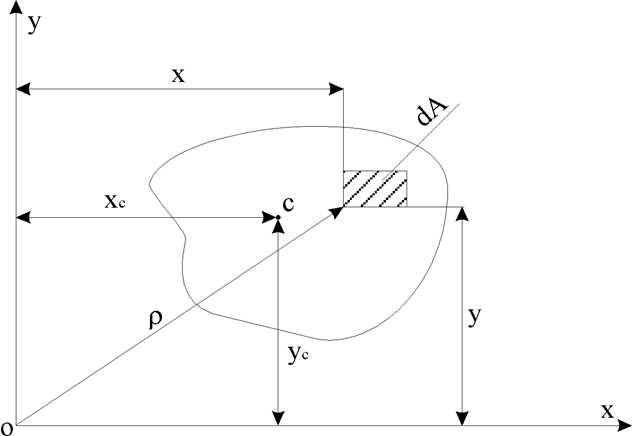 |
Рис.1
Свойства статического момента площади:
1. Статический момент площади измеряется в единицах длинны третьей степени (например, см 3 ).
2. Статический момент может быть меньше нуля, больше нуля и, следовательно, равняться нулю. Оси, относительно которых статический момент равен нулю, проходят через центр тяжести сечения и называются центральными осями.
Если xcиyc – координаты цента тяжести, то
3. Статический момент инерции сложного сечения относительно какой-либо оси равен сумме статических моментов составляющих простых сечений относительно той же оси.
Понятие статического момента инерции в науке о прочности используется для определения положения центра тяжести сечений, хотя надо помнить, что в симметричных сечениях центр тяжести лежит на пересечении осей симметрии.
2. Момент инерции плоских сечений ( фигур ) (моменты инерции второй степени).
а) осевой (экваториальный) момент инерции.
Осевым моментом инерции площади фигуры относительно какой-либо оси называется сумма произведений элементарных площадок на квадрат расстояния до этой оси распространения на всю площадь (рис. 1 )
Свойства осевого момента инерции.
1. Осевой момент инерции площади измеряется в единицах длинны четвертой степени (например, см 4 ).
2. Осевой момент инерции всегда больше нуля.
3. Осевой момент инерции сложного сечения относительно какой-либо оси равен сумме осевых моментов составляющих простых сечений относительно той же оси:
4. Величина осевого момента инерции характеризует способность стержня (бруса) определенного поперечного сечения сопротивляться изгибу.
б) Полярный момент инерции.
Полярным моментом инерции площади фигуры относительно какого-либо полюса называется сумма произведений элементарных площадок на квадрат расстояния до полюса, распространенная на всю площадь (рис. 1).
Свойства полярного момента инерции:
1. Полярный момент инерции площади измеряется в единицах длины четвертой степени ( например, см 4 ).
2. Полярный момент инерции всегда больше нуля.
3. Полярный момент инерции сложного сечения относительно какого-либо полюса (центра) равен сумме полярных моментов составляющих простых сечений относительно этого полюса.
4. Полярный момент инерции сечения равен сумме осевых моментов инерции этого сечения относительно двух взаимно перпендикулярных осей, проходящих через полюс.
5. Величина полярного момента инерции характеризует способность стержня (бруса) определенной формы поперечного сечения сопротивляться кручению.
в) Центробежный момент инерции.
ЦЕНТРОБЕЖНЫМ МОМЕНТОМ ИНЕРЦИИ площади фигуры относительно какой-либо системы координат называется сумма произведений элементарных площадок на координаты, распространенная на всю площадь (рис. 1)
Свойства центробежного момента инерции:
1. Центробежный момент инерции площади измеряется в единицах длинны четвертой степени (например, см 4 ).
2. Центробежный момент инерции может быть больше нуля, меньше нуля, и равняться нулю. Оси, относительно которых центробежный момент инерции равен нулю, называются главными осями инерции. Две взаимно перпендикулярные оси, из которых хотя бы одна является осью симметрии, будут главными осями. Главные оси, проходящие через центр тяжести площади, называются главными центральными осями, а осевые моменты инерции площади – главными центральными моментами инерции.
3. Центробежный момент инерции сложного сечения в какой-либо системе координат равен сумме центробежных моментов инерции составляющих фигур в той же схеме координат.
МОМЕНТЫ ИНЕРЦИИ ОТНОСИТЕЛЬНО ПАРАЛЛЕЛЬНЫХ ОСЕЙ.
 Рис.2
Рис.2
Дано: оси x, y – центральные;
т.е. осевой момент инерции в сечении относительно оси, параллельной центральной, равен осевому моменту относительно своей центральной оси плюс произведение площади на квадрат расстояния между осями. Отсюда следует, что осевой момент инерции сечения относительно центральной оси имеет минимальную величину в системе параллельных осей.
Сделав аналогичные выкладки для центробежного момента инерции, получим:
т.е. центробежный момент инерции сечения относительно осей, параллельных центральной системе координат, равен центробежному моменту в центральной системе координат плюс произведение площади на расстояние между осями.
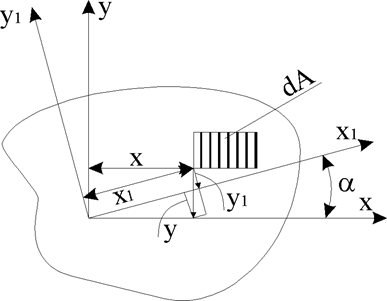
МОМЕНТЫ ИНЕРЦИИ В ПОВЕРНУТОЙ СИСТЕМЕ КООРДИНАТ
т.е. сумма осевых моментов инерции сечения есть величина постоянная, не зависит от угла поворота осей координат и равна полярному моменту инерции относительно начала координат. Центробежный момент инерции может менять свою величину и обращаться в «0».
Оси, относительно которых центробежный момент равен нулю будут главными осями инерции, а если они проходят через центр тяжести, то они называются главными осями инерции и обозначаются «u» и «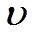
Моменты инерции относительно главных центральных осей называются главными центральными моментами инерции и обозначаются 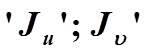
Пусть угол «a0» характеризует положение главных осей, тогда:
по этой зависимости определяем положение главных осей. Величину же главных моментов инерции после некоторых преобразований, определяем по следующей зависимости:
ПРИМЕРЫ ОПРЕДЕЛЕНИЯ ОСЕВЫХ МОМЕНТОВ ИНЕРЦИИ, ПОЛЯРНЫХ МОМЕНТОВ ИНЕРЦИИ И МОМЕНТОВ СОПРОТИВЛЕНИЯ ПРОСТЕЙШИХ ФИГУР.
1. Прямоугольное сечение
Оси x и y – здесь и в других примерах – главные центральные оси инерции.
Определим осевые моменты сопротивления:
2. Круглое сплошное сечение. Моменты инерции.
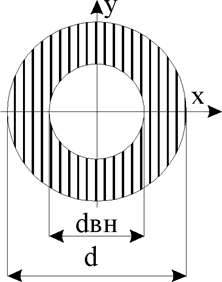
3. 
Геометрические характеристики плоских сечений
При деформации изгиба и кручения прочность и жесткость характеризуются не только размерами сечения, но и его формой. К числу геометрических характеристик сечения, учитывающих оба указанных фактора, относятся статические моменты, моменты инерции, моменты сопротивления. Различают осевые, полярные и центробежные моменты инерции.
Осевым моментом инерции сечения называют взятую по всей площади сечения сумму произведений элементарных площадок на квадраты их расстояний до соответствующей оси. Обозначая моменты у инерции относительно осей z и y соответственно через Jz и Jy, имеем:
Полярным моментом инерции (моментом инерции относительно полюса) называют взятую по всей площади сечения сумму произведений элементарных площадок на квадраты их расстояний до данного полюса:
Центробежным моментом инерции сечения называют взятую по всей площади сечения сумму произведений элементарных площадок на обе координаты в данной прямоугольной системе осей. Обозначая центробежный момент инерции через Jzy имеем:
Из приведенных определений следует, что момент инерции сложной фигуры равен сумме моментов инерции ее частей.
Рассмотрим некоторые свойства моментов инерции.
1. Момент инерции относительно полюса, являющегося началом прямоугольной системы координат, равен сумме моментов инерции относительно осей данной системы.
2. Момент инерции сечения относительно какой-либо оси равен моменту инерции этого сечения относительно центральной оси, параллельной данной, сложенному с произведением площади сечения на квадрат расстояния между осями.
Рассмотрим понятие о главных осях инерции. Две взаимно перпендикулярные оси с началом в данной точке, для которых центробежный момент инерции плоской фигуры равен нулю, называют главными осями инерции фигуры в этой точке. Глазные оси инерции в центре тяжести фигуры называют главными центральными осями инерции.
Легко показать, что в том случае, когда фигура имеет хотя бы одну ось симметрии, эта ось является одной из главных центральных осей инерции, а другая проходит через центр тяжести фигуры перпендикулярно первой. Если хотя бы одна из двух взаимно перпендикулярных осей, проходящих через центр тяжести сечения, является осью симметрии, то такие оси являются главными центральными осями инерции. Для таких сечений, как круг и кольцо любые две взаимно перпендикулярные центральные оси являются главными осями инерции.
В общем случае главные центральные оси инерции фигуры могут быть найдены, если известны ее центробежный Jzy и осевые Jz и Jy моменты инерции относительно произвольно расположенных центральных осей z и у. Для этого систему осей z1 и у1 необходимо повернуть на угол 
Моменты инерции относительно главных центральных осей инерции называют главными моментами инерции: они обладают тем свойством, что один из них имеет максимальное, а другой минимальное значение по сравнению с моментами инерции относительно остальных центральных осей. Главные моменты инерции
Значения моментов инерции простейших фигур, а также прокатных профилей можно найти в технических справочниках или вычислить по приведенным выше формулам.
Определим величины моментов инерции наиболее распространенных плоских сечений, встречающихся при расчетах и конструировании деталей механизмов.
1. Прямоугольник высотой h и шириной b (Рис. 92),
а). Выделим в прямоугольнике элементарную полоску высотой dy и шириной Ь. Полоска отстоит от центральной оси г, параллельной основанию на расстоянии у, При этом у изменяется в пределах
При определении момента инерции относительно оси y имеем
Круговое кольцо с наружным диаметром D и внутренним d.
В данном случае полярный момент инерции может быть получен как разность полярных моментов инерции большого и малого круга (рис.92, в).
Растяжение и сжатие
Растяжение (сжатие) – это вид деформации, при котором в поперечном сечении стержня возникает только продольная растягивающая (сжимающая) сила.
В условиях растяжения находится стержень под действием осевых сил на краях (рис. 93)
Передача такого усилия к стержню может осуществляться различными способами, например, через гайку и головку болта в резьбовом соединении. Но во всех случаях равнодействующая внешних сил будет равна F.
Модель растягиваемого стержня используется в расчетах болтов, ремней передач, стержней ферм, лопаток турбин и т. д.
При осевом растяжении и сжатии внутренние силы в поперечном сечении могут быть заменены одной силой, направленной вдоль оси стержня (рис. 94) — продольной силой N. В случае когда сила направлена к отброшенной части наружу, имеет место растяжение (рис. 94, a). Наоборот, если она направлена от отброшенной части внутрь (рис. 94, б), имеет место сжатие. Будем считать силу N положительной, если она растягивает стержень, и отрицательной – если сжимает.
Рассмотрим пример (рис.95, а).
Здесь сила F приложена в сечении x = a. В любом сечении при x1 ≥ a (рис.95, б) N(x1) = 0. Это означает, что часть стержня на этом участке под силой F не нагружена. Проведем второе сечение x2 ≤ a (рис. 95, в) и рассмотрим равновесие нижней части. Уравнение равновесия относительно оси x:



График изменения внутренних сил (эпюра) приведен на рис. 95, г. Каждая ордината эпюры равна значению N в данном сечении. Эпюру строят на линии, проведенной параллельно оси стержня.
Нормальное напряжение в поперечном сечении стержня при растяжении равно поделенной на площадь сечения продольной силе в этом сечении:

Таким образом, часть стержня, находящаяся под силой F не напряжена.
При сжатии стержня напряжения имеют лишь другой (отрицательный) знак (нормальная сила направлена в тело стержня).
Под действием осевых растягивающих сил стержень постоянного сечения площадью 

где l 1, l 0 − длины стержня в деформированном и недеформированном состоянии, ∆l − абсолютное (полное) удлинение при растяжении (в случае сжатия данная величина называется абсолютным (полным) укорочением).
Экспериментально установлено, что чем больше l 0, тем больше ∆l. Наиболее удобной мерой деформации является относительное удлинение— удлинение, отнесенное к первоначальной длине стержня,

Величина ε обычно выражается в процентах от начальной длины. При сжатии ε называют относительным укорочением.
Из опыта следует, что удлинение стержня в осевом направлении сопровождается уменьшением его поперечных размеров. Следовательно, при растяжении и сжатии возникает не только продольная, но и поперечная деформация стержня.
Если первоначальная ширина стержня a0, то под действием сил F она уменьшится на величину

Относительная поперечная деформация будет определяться выражением

Знак “минус” показывает, что при растяжении стержня поперечные размеры уменьшаются.
Отношение поперечной деформации к продольной при растяжении (сжатии), взятое по абсолютной величине, называюткоэффициентом Пуассона:

На основании экспериментов получено: для сталей μ = 0,25. 0,3; для алюминиевых сплавов μ = 0,3. 0,35; для медных сплавов μ = 0,35.
Между напряжениями и малыми деформациями существует линейная зависимость, называемая законом Гука. Для центрального растяжения (сжатия) она имеет вид

где E — коэффициент пропорциональности, именуемый модулем упругости (модулем Юнга). По физическому смыслу модуль упругости — напряжение, которое вызывает деформацию ε = 1 (удлинение стержня, равное первоначальной длине). По данным экспериментов: E = (2. 2,2)∙10 5 МПа — для сталей; E = 1,1∙10 5 МПа — для титановых сплавов; E = 0,7∙10 5 МПа—для алюминиевых сплавов.
Для некоторых материалов (например, коррозионно-стойких сталей) закон Гука является приближенным даже при сравнительно небольших деформациях.
С учетом выражений (1) и (3) закон Гука для растянутого (сжатого) стержня (7) можно записать в виде

где μ — коэффициент продольной податливости стержня, показывающий удлинение (укорочение) стержня, вызываемое растягивающей (сжимающей) силой F = 1 Н. Произведение E A называют жесткостью сечения стержня при растяжении (сжатии).
Для стержня переменного (ступенчатого) сечения удлинения определяют по участкам (ступеням) и результаты суммируют алгебраически:

При расчете упругих перемещений стержня от нескольких сил часто применяют принцип независимости действия сил: перемещение стержня от действия группы сил может быть получено как сумма перемещений от действия каждой силы в отдельности.
Экспериментально установлено, что модуль упругости E при умеренном нагреве незначительно меняется с температурой, а коэффициент α практически не зависит от напряжения σ. Для стали эта зависимость имеет место до температуры 300. 400 ° С. При более высоких температурах необходимо учитывать зависимость модуля упругости E от температуры t.
Следует отметить, что формулы (7). (8) выведены в предположении, что стержень растянут силами, равномерно распределенными по сечению (рис. 96, а).
При растяжении сосредоточенными силами, как показывают эксперименты и расчеты методами теории упругости, сечения стержня вблизи мест приложения внешних сил в результате деформации искривляются (рис.96,б) возникают большие местные деформации и напряжения.
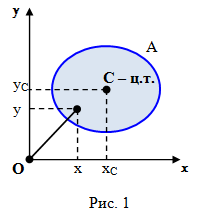
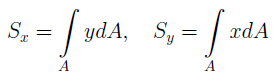
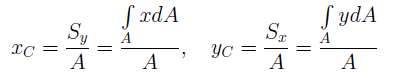
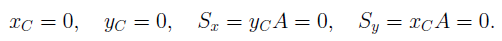
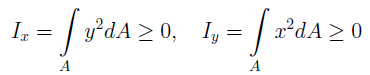
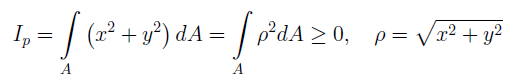
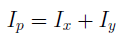
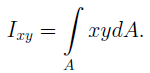
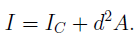
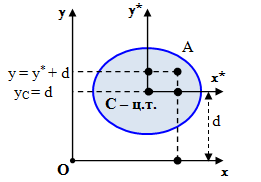
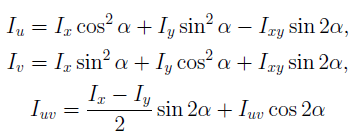
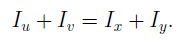
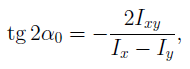
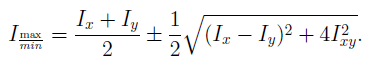
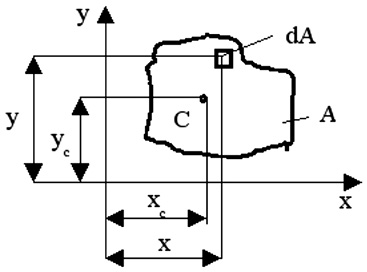
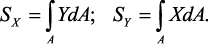
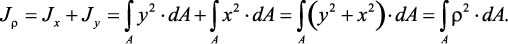
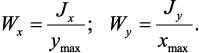
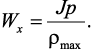
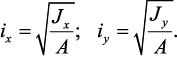
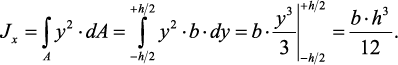
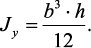



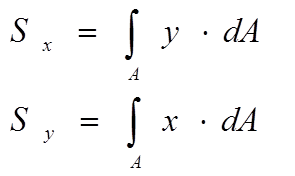
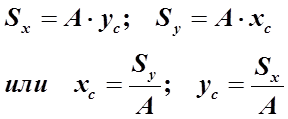
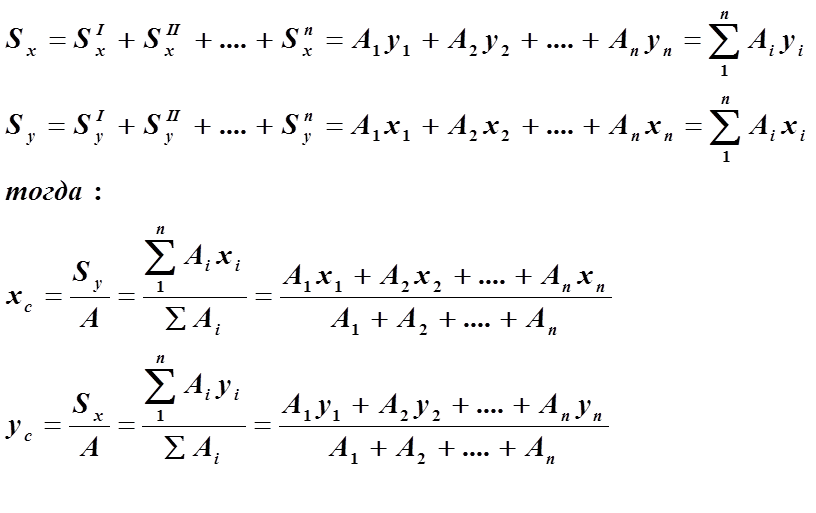
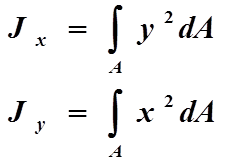
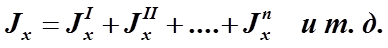
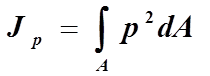
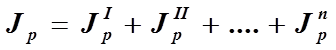
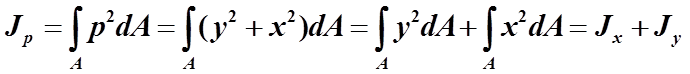
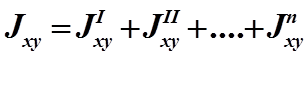
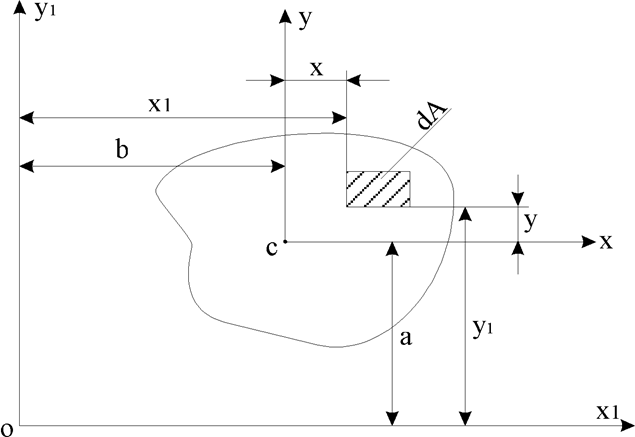 Рис.2
Рис.2