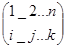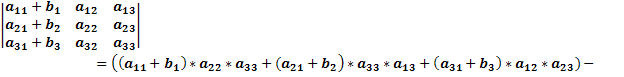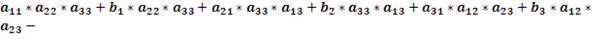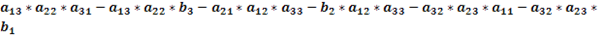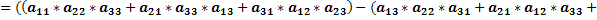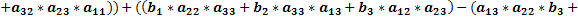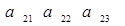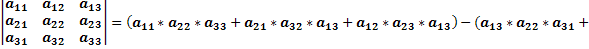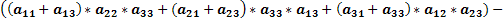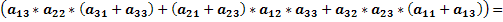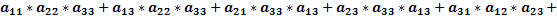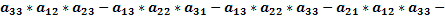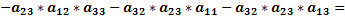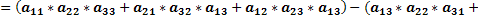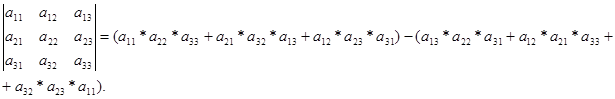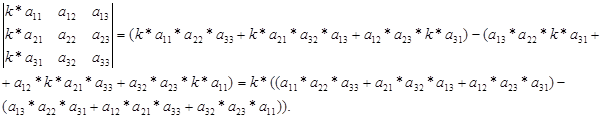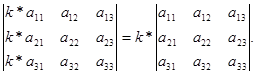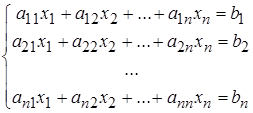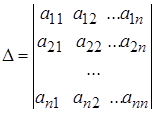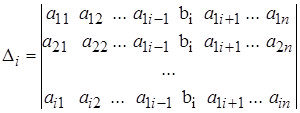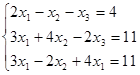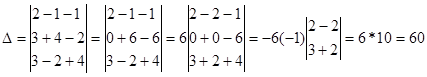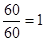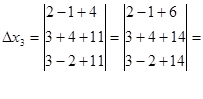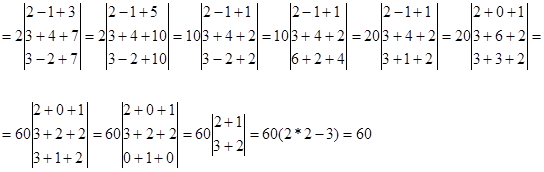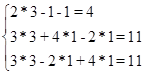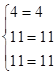Доказать что определитель делится на

Математический портал

Nav view search

Navigation

Search

Вычисление определителей 2-го и 3-го порядков. Миноры, алгебраические дополнения.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

— квадратная матрица 3-го порядка, то соответсвующим ей определителем 3-го порядка называется число

Примеры.

Вычислить определители второго порядка:

Решение.

Ответ: 18.

Решение.

3.8. Решить уравнение:

Решение.

Решение.

Решение.

2) Если все элементы строки (столбца) умножить на одно и тоже число, то определитель умножится на это число.

3) Если поменять местами две строки (столбца), то определитель поменяет знак. В частности, если две строки (столбца) равны, то определитель равен нулю.

5) Если одна строка (столбец) является линейной комбинацией других строк (столбцов), то определитель равен нулю.

6) Определитель не меняется если к одной из его строк (столбцов) добавить линейную комбинацию его других строк (столбцов).

Примеры:

Доказательство.

Что и требовалось доказать.

Проверка.

1) Пользуясь 6-м свойством определителей от первого столбца отнимаем второй, а затем используем 2-е свойство и выносим общий множетель за определитель.

Метод приведения к треугольному виду заключается в преобразовании определителя, когда все элементы, лежащие по одну сторону одной из ее диагоналей, становятся равными нулю. В этом случае определитель равен произведению диагональных элементов.

Примеры.

Вычислить определители, используя подходящее разложение по строке или столбцу.

Решение.

Решение.

Вычислим этот определитель с помощью приведения определителя к треугольному виду:

Домашнее задание:

Вычислить определители второго порядка:

Вычислить определители 3-го порядка:

Вычислить определители, используя подходящее разложение по строке или столбцу.

Источник

Основные свойства определителей

1.При транспонировании матрицы ее определитель не меняется.

2.Если в определителе поменять местами две строки (столбца), то определитель при этом лишь поменяет знак.

3.Если каждый элемент какой-либо строки (столбца) определителя представлен в виде суммы двух слагаемых, то определитель равен сумме двух определителей, в первом из которых в той же строке (столбце) записано первое слагаемое, во втором – второе, а все остальные строки (столбцы) этих двух определителей совпадают с соответствующими строками (столбцами) исходного определителя.

4.Если в определителе все элементы какой-либо строки (столбца) умножить на число, то и определитель умножится на это число. Или: общий множитель строки или столбца можно выносить за знак определителя.

5.Если определитель содержит строку или столбец, полностью состоящий из нулей, то он равен нулю.

6.Если определитель содержит две пропорциональные строки (столбца), то он равен нулю.

7.Если к какой-либо строке (столбцу) определителя прибавить другую его строку (столбец), умноженную на число, то определитель при этом не изменится.

Следствие. Если к какой-либо строке (столбцу) определителя прибавить линейную комбинацию других его строк (столбцов), то определитель при этом не изменится.

8.Определитель произведения матриц равен произведению их определителей, т. е. .

9. Пример 10. 16.Вычислить определители:

а) ; б) .

∆ а) Представим элементы второго столбца в виде суммы: 12421=12321+100, 21424=21324+100. Тогда:

[применяем третье свойство]

[к первому определителю применяем

шестое свойство, а ко второму – четвертое]

.

б) Умножим первый столбец на (–1) и прибавим сначала ко второму, а затем и к третьему столбцу. На основании 7-го свойства значение определителя не изменится, а сам он примет следующий вид:

Элементы третьего столбца последнего определителя пропорциональны соответствующим элементам второго, поэтому он равен нулю, а значит, равен нулю и исходный определитель. ▲

Пример 10.17. Известно, что числа 20604, 53227, 25755, 20927 и 78421 делятся на 17. Доказать, что следующий определитель также делится на 17:

.

∆ Заметим, что в строках определителя записаны цифры, составляющие приведенные числа. Чтобы получить из цифр само число следует к последней цифре прибавить предыдущую, умноженную на 10, третью, умноженную на 100, вторую, умноженную на 1000 и, наконец, первую, умноженную на 10000. Применим те же действия к столбцам определителя: к последнему столбцу прибавим четвертый, умноженный на 10, третий, умноженный на 100, второй, умноженный на 1000 и, наконец, первый, умноженный на 10000. В результате в последнем столбце окажутся как раз те числа, которые по условию делятся на 17. На основании 4-го свойства определитель также делится на 17. ▲,

Tеорема 10.1. Если в определителе выбрать какую-либо строку (столбец), то определитель равен сумме произведений элементов этой строки (столбца) на их алгебраические дополнения, т. е.

–

разложение по -й строке,

–

разложение по -му столбцу.

Следствие. Определитель диагональной или треугольной матрицы равен произведению ее диагональных элементов.

Пример 10. 18.Вычислить определитель

двумя способами: а) по определению; б) используя теорему 10.1.

∆ а) Разлагаем определитель по первой строке:

(определители третьего порядка также вычислялись методом разложения по первой строке, известному из аналитической геометрии).

Замечание. При разложении определителя по строке или столбцу каждый элемент умножается на свое алгебраическое дополнение. Если же элемент равен нулю, то это алгебраическое дополнение и считать не надо, все равно при умножении нуль получим. Так, при разложении по первой строке мы не считали алгебраическое дополнение ко второму элементу.

б) В рассматриваемом определителе второй столбец имеет только один отличный от нуля элемент, поэтому и вычислять его выгодно разложением именно по второму столбцу: остается только одно слагаемое:

.▲

Если считать определитель пятого порядка, разлагая его непосредственно по какой-либо строке или столбцу, мы получим пять определителей четвертого порядка, каждый из них распадается на четыре определителя третьего порядка. Таким образом, вычисление определителя пятого порядка приводит к двадцати определителям третьего! При решении примера 10.18 мы заметили, что вычисления существенно упрощаются, если определитель содержит строку или столбец, имеющий не более одного отличного от нуля элемента. Этого всегда можно добиться, применяя следующий

Дата добавления: 2015-07-19 ; просмотров: 723 | Нарушение авторских прав

Источник

Линейная алгебра: Даны числа 1081, 1403, 2093, 1541, которые делятся на 23.

Для просмотра формул ваш браузер должен поддерживать MathML.

Помогите решить пожалуйста:
Даны числа 1081, 1403, 2093, 1541, которые делятся на 23.

Доказать, почему det матрицы :
1 0 8 1
1 4 0 3
2 0 9 3
1 5 4 1
делится на 23 тоже.

Редактировалось 2 раз(а). Последний 12.11.2009 20:23.

помогите ещё: каким способом легче всего вычислить детерминант симметрической матрицы типа:

$\left(\begin x_1 & a & b \\ a & x_2 & c \\ b & c & x_3 \end\right)$

Редактировалось 3 раз(а). Последний 12.11.2009 21:02.

Редактировалось 1 раз(а). Последний 12.11.2009 21:02.

Цитата
sidi98765
Помогите решить пожалуйста:
Даны числа 1081, 1403, 2093, 1541, которые делятся на 23.

Доказать, почему det матрицы :
1 0 8 1
1 4 0 3
2 0 9 3
1 5 4 1
делится на 23 тоже.

Редактировалось 1 раз(а). Последний 12.11.2009 21:03.

Цитата
sidi98765
Помогите решить пожалуйста:
Даны числа 1081, 1403, 2093, 1541, которые делятся на 23.

Доказать, почему det матрицы :
1 0 8 1
1 4 0 3
2 0 9 3
1 5 4 1
делится на 23 тоже.

Ее определитель будет равен произведению собственных значений. Поэтому, если Вы умеете простым способом найти собственные значения, то и определитель мгновенно сыщется.

Редактировалось 1 раз(а). Последний 13.11.2009 11:04.

Источник

Доказательства свойств определителя

Свойство №1: Определитель не изменяется при транспортировании матриц (строк и столбцов).

Доказательство:

Опр. Матрицы A_ji называется транспонированной матрицей A_ij

= det A = det A T

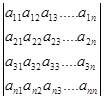
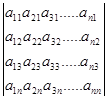
Выберем любое слагаемое из суммы определителя.

Следовательно определители равны.

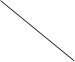
Свойство №2: Если один из столбцов (строк) состоит из нулей, то определитель равен нулю.

Доказательство:

Пусть дана матрица, один столбец которой равен 0.

=detA подсчитаем определитель данной матрицы.

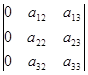
Подсчитаем определитель данной матрицы, используя правило равнобедренных треугольников, основания которых параллельны главной и побочной диагоналям.

=0*а₂₂*а₃₃+а₁₂*а₂₃*0+а₃₂*а₁₃*0 = 0

=-(а₁₃*а₂₂*0+а₁₂*а₃₃*0+а₂₃*а₃₂*0)=0

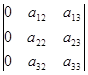
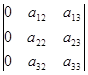
Свойство №3: Если один из определителей получен из другого определителя перестановкой двух столбцов (строк), то определители отличаются друг от друга знаком.

Доказательство:Возьмём матрицу определитель которой равен detA и переставим в ней 2 столбца. Получим:

,после перестановки получим: .

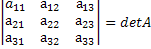
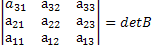
Посчитаем определители обеих матриц. Получим:

Получили, что det A=-det B.

Свойство №4: Если все элементы какого-либо i-го столбца (строки) определителя являются суммами двух слагаемых, то такой определитель равен сумме двух определителей в первом из которых в качестве i-го столбца (строки) взяты первые слагаемые, а во втором – вторые слагаемые; при этом элементы всех остальных строк (столбцов) у каждого из трёх определителей одинаковы.

Доказательство:

Возьмём матрицу, в которой элементы первого столбца равны a_ij+b_j и посчитаем её определитель.

.

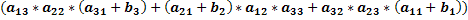
Раскроем скобки и приведём подобные слагаемые.

.

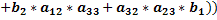
То есть: .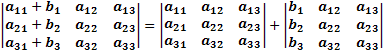

Свойство №5: Определитель, содержащий два пропорциональных, в частности два равных, столбца (строки), равен нулю.

Доказательство:

Пусть дан определитель detA≠0, содержащий две равные строки.

= detA ; =

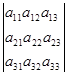
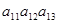
Поменяем местами эти равные строки. Получим новый определитель.

.

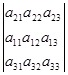
Так как данный определитель получен из определителя detA перестановкой строк, то из предыдущего свойства следует, что полученный определитель принимает значение –detA. В то же время, количество слагаемых и модуль значений определителей detA и –detA равны, то справедливо будет равенство detA=-detA. Из данного равенства следует что detA=0. Свойство доказано.

Свойство №6: Определитель не меняется, если к какому-нибудь столбцу (строке) прибавить линейную комбинацию других столбцов (строк).

Доказательство:

Возьмём матрицу коэффициентов и посчитаем её определитель.

Прибавим к первому столбцу третий. Получим новую матрицу.

.

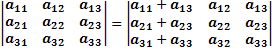
Посчитаем её определитель.

.

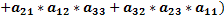
Свойство №7: Если все элементы какого-нибудь столбца (строки) определителя умножить на некоторое число k, то есть весь определитель умножается на k, то общий множитель любой строки или любого столбца можно выносить за знак определителя.

Доказательство:Возьмём матрицу и посчитаем её определитель.

То есть.

5. Пример применения правила Крамера для решения систем n уравнений с n неизвестными

Определители очень широко используются при решении и исследовании систем линейных n уравнений с n неизвестными. Правило решения такой системы с помощью определителей называется правилом Крамера. Покажем это правило на примере.

Правило Крамера: правило решения системы n линейных уравнений. с n неизвестными, определитель которой отличен от нуля, всегда имеет решение. Это решение единственное и определяется таким правилом Крамера: значение каждого из неизвестных 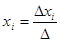, где — определитель системы., матрица которого составлена из коэффициентов при неизвестных системы, а _I – определитель, матрица которого получена заменой столбца коэффициентов при данном неизвестном на столбец свободных членов системы. В случае если определитель системы равен нулю, система имеет бесконечно много решений.

Пусть дана система из трех уравнений с тремя неизвестными:

Посчитаем определитель матрицы системы, составленной из коэффициентов при неизвестных:

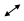
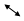
После подсчета определителя системы, подсчитаем определители неизвестных. Для этого вырезаем из столбец данной переменной, а на его место ставим столбец свободного члена.

= = = 6 = 6 = 6*(4*2-(-2)*11)=180

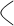
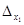
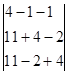
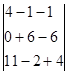
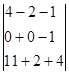
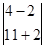
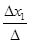
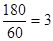
Согласно правилу Крамера значение неизвестной переменной равно частному от определителя данной неизвестной и определителя системы. Значит переменная x_{1= ;} x₁= .

Действуя по тому же алгоритму, найдем значения переменных x₂ и x₃:

По правилу равнобедренных треугольников, основания которых параллельны главной и побочной диагоналям матрицы получим:

= 2*11*4+3*11*(-1)+4*(-2)*3= 88-33-24=31 =60

-2*(-2)*11-3*4*4 – (-1)*11*3= 44-48+33=29

Значит x₂=

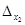
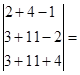
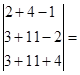
Значит x₃=

Для доказательства истинности правила Крамера, проверим полученные значения переменных, подставив полученные значения в систему:

После подстановки мы получили верное числовое равенство, значит, правило Крамера истинно для решения системы n уравнений с n неизвестными. Ответ: (3;1;1)

Глава 2.Векторное произведение

Источник