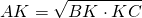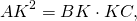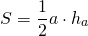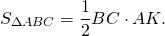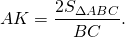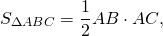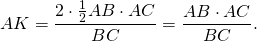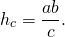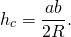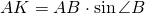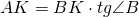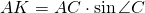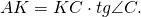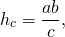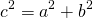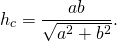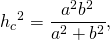Доказать что высота прямоугольного треугольника
Свойства высоты прямоугольного треугольника
В данной публикации мы рассмотрим основные свойства высоты в прямоугольном треугольнике, а также разберем примеры решения задач по этой теме.
Примечание: треугольник называется прямоугольным, если один из его углов является прямым (равняется 90°), а два остальных – острые ( Содержание скрыть
Свойства высоты в прямоугольном треугольнике
Свойство 1
В прямоугольном треугольнике две высоты (h1 и h2) совпадают с его катетами.
Третья высота (h3) опускается на гипотенузу из прямого угла.
Свойство 2
Ортоцентр (точка пересечения высот) прямоугольного треугольника находится в вершине прямого угла.
Свойство 3
Высота в прямоугольном треугольнике, проведенная к гипотенузе, делит его на два подобных прямоугольных треугольника, которые также подобны исходному.
3. △ABD ∼ △ADC по двум равным углам: ∠ABD = ∠DAC, ∠BAD = ∠ACD.
Доказательство: ∠BAD = 90° – ∠ABD (ABC). В то же время ∠ACD (ACB) = 90° – ∠ABC. Следовательно, ∠BAD = ∠ACD.
Аналогичным образом доказывается, что ∠ABD = ∠DAC.
Свойство 4
В прямоугольном треугольнике высота, проведенная к гипотенузе, вычисляется следующим образом:
1. Через отрезки на гипотенузе, образованные в результате ее деления основанием высоты:
2. Через длины сторон треугольника:
Данная формула получена из Свойства синуса острого угла в прямоугольном треугольнике (синус угла равен отношению противолежащего катета к гипотенузе) :
Примечание: к прямоугольному треугольнику, также, применимы общие свойства высоты, представленные в нашей публикации – “Высота в треугольнике abc: определение, виды, свойства”.
Пример задачи
Задача 1
Гипотенуза прямоугольного треугольника поделена высотой, проведенной к ней, на отрезки 5 и 13 см. Найдите длину этой высоты.
Решение
Воспользуемся первой формулой, представленной в Свойстве 4:
Задача 2
Катеты прямоугольного треугольника равны 9 и 12 см. Найдите длину высоты, проведенной к гипотенузе.
Решение
Для начала найдем длину гипотенузы по теореме Пифагора (пусть катеты треугольника – это “a” и “b”, а гипотенуза – “c”):
c 2 = a 2 + b 2 = 9 2 + 12 2 = 225.
Следовательно, с = 15 см.
Теперь можно применить вторую формулу из Свойства 4, рассмотренного выше:
Высота прямоугольного треугольника, проведенная к гипотенузе
Пример задачи
Задача 1 Гипотенуза прямоугольного треугольника поделена высотой, проведенной к ней, на отрезки 5 и 13 см. Найдите длину этой высоты.
Решение Воспользуемся первой формулой, представленной в Свойстве 4:
Задача 2 Катеты прямоугольного треугольника равны 9 и 12 см. Найдите длину высоты, проведенной к гипотенузе.
Решение Для начала найдем длину гипотенузы по теореме Пифагора (пусть катеты треугольника – это “a” и “b”, а гипотенуза – “c”):c 2 = a 2 + b 2 = 9 2 + 12 2 = 225. Следовательно, с = 15 см.
Теперь можно применить вторую формулу из Свойства 4, рассмотренного выше:
Видео
Признаки подобия прямоугольных треугольников
Признаков подобия прямоугольных треугольников тоже немного.
Только три — по острому углу, по двум катетам и по катету и гипотенузе.
Также смотри на рисунки и ты сразу все поймешь и запомнишь.
И сможешь применять при решении задач!
Свойства высоты в равностороннем треугольнике
Равносторонний треугольник — это треугольник, стороны которого, углы, высоты, медианы, оси симметрии и биссектрисы будут равны.
Такой треугольник является частным примером равнобедренного треугольника, но не наоборот.
Высоту в таком треугольнике можно найти с помощью следующей формулы:
h=a32 где а — сторона равностороннего треугольника.
Главным свойством, которым обладает высота равностороннего треугольника, является тот факт, что она равна медиане и биссектрисе:
а — сторона правильного равностороннего треугольника.
Бонус: Равнобедренные треугольники вебинар из курса подготовки к ЕГЭ
В этом видео мы вспомним все свойства равнобедренных треугольников и научимся их применять в задачах из ЕГЭ.
Очень часто все «проблемы» с решением задач на равнобедренный треугольник решаются построением высоты.
Также мы научимся решать и «обычные» треугольники. Убедимся в достоверности утверждении из прошлого урока о прямоугольных треугольниках — очень часто решение задач сводится к нескольким прямоугольным треугольникам.
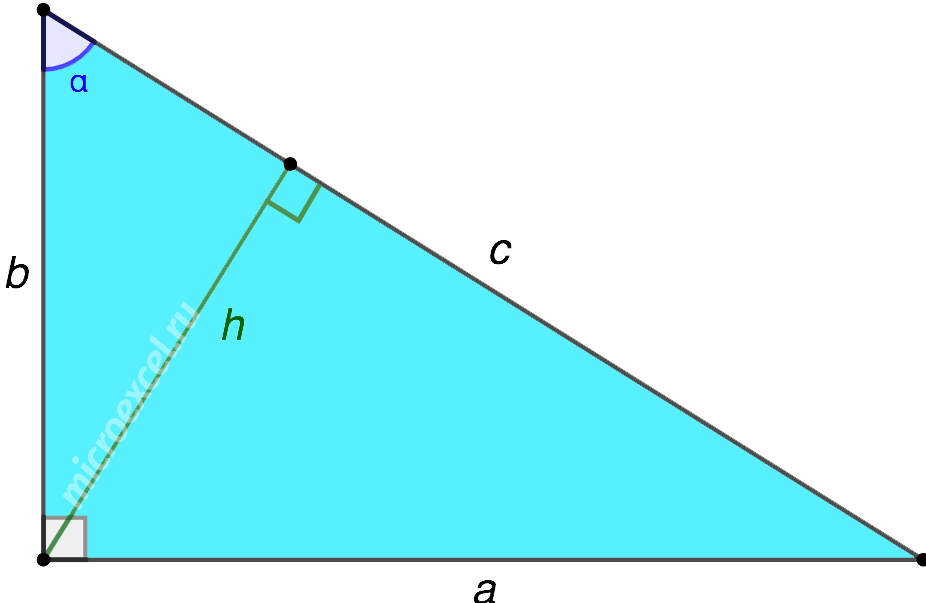
Высота в прямоугольном треугольнике
Вспомним, что высота треугольника — это перпендикуляр, опущенный из его вершины на противоположную сторону.
В прямоугольном треугольнике катеты являются высотами друг к другу. Главный интерес представляет высота, проведённая к гипотенузе.
Один из типов экзаменационных задач банке заданий ФИПИ — такие, где в прямоугольном треугольнике высота проведена из вершины прямого угла. Посмотрим, что получается:
Иными словами, каждый из трех углов треугольника равен одному из углов треугольника (и треугольника ). Треугольники и называются подобными. Давайте нарисуем их рядом друг с другом.
Они отличаются только размерами. Стороны подобных треугольников пропорциональны. Что это значит?
Ты нашел то, что искал? Поделись с друзьями!
(поскольку значение синуса острого угла положительно). Тогда:
Нам известно также, что:
Решая эту систему из двух уравнений, найдем:
Запишем площадь треугольника АВС двумя способами:
Найти высоту, проведенную из вершины прямого угла, можно было и другим способом. Мы выбрали самый короткий путь — составили и решили систему уравнений.
Подобие в прямоугольном треугольнике
Рассмотрим подобие треугольников в прямоугольном треугольнике.
Высота прямоугольного треугольника, проведённая к гипотенузе, делит треугольник на два треугольника, каждый из которых подобен данному. Эти треугольники также подобны между собой.


Аналогично, для треугольников CBH и ABC угол B — общий. Следовательно, ∆CBH∼∆ABC.
2) Так как сумма острых углов прямоугольного треугольника равна 90º, в треугольнике ABC ∠B=90º-∠A, в треугольнике CHB ∠BCH=90º-∠B=90º-(90º-∠A)=∠A.
Таким образом, в треугольниках ACH и CBH ∠CAH=∠BCH. А значит, ∆ACH ∼∆CBH (по острому углу).
(Другой вариант: два треугольника, подобных одному треугольнику, подобны между собой).
Прямые, параллельные катетам прямоугольного треугольника, отсекают от него треугольники, подобные данному. Эти треугольники также подобны между собой.

1) Так как ∠C=90º и KF∥BC, то ∠AKF=90º, то есть треугольник AFK — прямоугольный.
Для треугольников AFK и ABC угол A — общий. Следовательно, ∆AFK ∼∆ABC (по острому углу).
2) Аналогично, ∠MNB=90º и ∆MBN ∼∆ABC (по общему острому углу B).
3) ∠AFK=∠B (как соответственные при KF∥BC и секущей AB). Следовательно, ∆AFK∼∆MBN (по острому углу).
Высота прямоугольного треугольника
Высота прямоугольного треугольника, проведенная к гипотенузе, может быть найдена тем или иным способом в зависимости от данных в условии задачи.

или, в другой записи,
где BK и KC — проекции катетов на гипотенузу (отрезки, на которые высота делит гипотенузу).
Высоту, проведенную к гипотенузе, можно найти через площадь прямоугольного треугольника. Если применить формулу для нахождения площади треугольника
(половина произведения стороны на высоту, проведенную к этой стороне) к гипотенузе и высоте, проведенной к гипотенузе, получим:
Отсюда можем найти высоту как отношение удвоенной площади треугольника к длине гипотенузы:
Так как площадь прямоугольного треугольника равна половине произведения катетов:
То есть длина высоты, проведенной к гипотенузе, равна отношению произведения катетов к гипотенузе. Если обозначить длины катетов через a и b, длину гипотенузы — через с, формулу можно переписать в виде
Так как радиус окружности, описанной около прямоугольного треугольника, равен половине гипотенузы, длину высоты можно выразить через катеты и радиус описанной окружности:
Поскольку проведенная к гипотенузе высота образует еще два прямоугольных треугольника, ее длину можно найти через соотношения в прямоугольном треугольнике.
Из прямоугольного треугольника ABK
Из прямоугольного треугольника ACK
Длину высоты прямоугольного треугольника можно выразить через длины катетов. Так как
по теореме Пифагора
Если возвести в квадрат обе части равенства:
можно получить еще одну формулу для связи высоты прямоугольного треугольника с катетами: