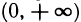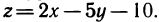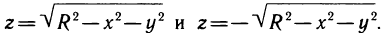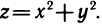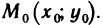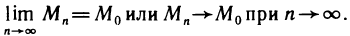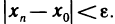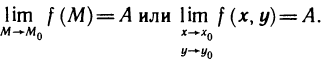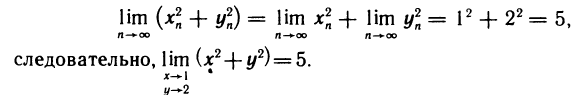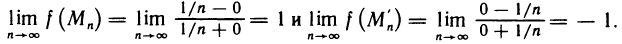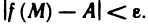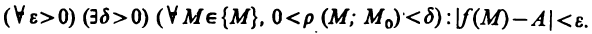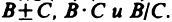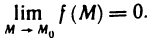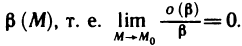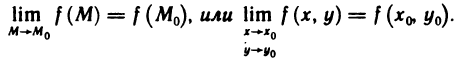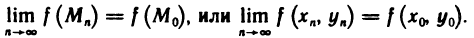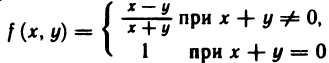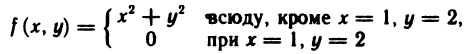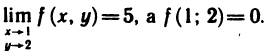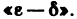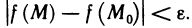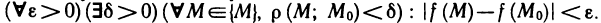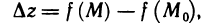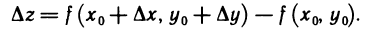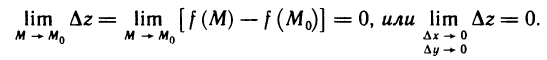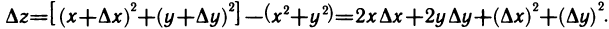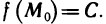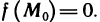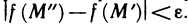Доказать по определению что предел функции двух переменных
Предел функции нескольких переменных
Определение функции нескольких переменных. Основные понятия.
Если каждой паре независимых друг от друга чисел (х,у) из некоторого множества по какому-либо правилу ставится в соответствие одно значение переменной z, то она называется функцией двух переменных. z=f(x,y,)
Множество значений (область значений) функции – все значения, которые принимает функция в ее области определения.
Окрестность точки M0 (х0;y0) радиуса r – совокупность всех точек (x,y), которые удовлетворяют условию 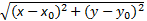
| f (x, y) – A | 0 найдется δ-окрестность точки (х0, у0) такая, что для всех (x, y) из этой окрестности, отличных от (х0, у0), выполняется неравенство (3).
Так как координаты произвольной точки (x, y) окрестности точки (х0, у0) можно записать в виде х = х0 + Δх, у = у0 + Δу, то равенство (1) эквивалентно следующему равенству:
Рассмотрим некоторую функции, заданную в окрестности точки (х0, у0), кроме, быть может, самой этой точки.
Пусть ω = (ωх, ωу) – произвольный вектор длины единица (|ω| 2 = ωх 2 + ωу 2 = 1) и t > 0 – скаляр. Точки вида

Число А называется пределом функции f(M) при М → М0, если для любого числа ε > 0 всегда найдется такое число δ > 0, что для любых точек М, отличных от М0 и удовлетворяющих условию | ММ0 |
и на этом языке определить непрерывность f в (x, y): функция f непрерывна в точке (x, y), если

Теорема. Сумма, разность, произведение и частное непрерывных в точке (х0,у0) функций f и φ есть непрерывная функция в этой точке, если, конечно, в случае частного φ (х0, у0) ≠ 0.
Постоянную с можно рассматривать как функцию f (x, y) = с от переменных x,y. Она непрерывна по этим переменным, потому что
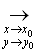
Следующими по сложности являются функции f (x, y) = х и f (x, y) = у. Их тоже можно рассматривать как функции от (x, y), и при этом они непрерывны. Например, функция f (x, y) = х приводит в соответствие каждой точке (x, y)число, равное х. Непрерывность этой функции в произвольной точке (x, y)может быть доказана так:


Если производить над функциями x, y и постоянными действия сложения, вычитания и умножения в конечном числе, то будем получать функции, называемые многочленами от x, y. На основании сформулированных выше свойств многочлены от переменных x, y – непрерывные функции от этих переменных для всех точек (x, y) 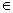
Отношение P/Q двух многочленов от (x, y) есть рациональная функция от (x,y), очевидно, непрерывная всюду на R2, за исключением точек (x, y), где Q(x, y) = 0.
может быть примером многочлена от (x, y) третьей степени, а функция
есть пример многочлена от (x, y) четвертой степени.
Приведем пример теоремы, утверждающей непрерывность функции от непрерывных функций.
Тогда функция F (u, v) = f [ φ (u, v), ψ (u, v), χ (u, v) ] непрерывна (по
Доказательство. Так как знак предела можно внести под знак характеристики непрерывной функции, то
Теорема. Функция f (x, y), непрерывная в точке (х0, у0) и не равная нулю в этой точке, сохраняет знак числа f (х0, у0) в некоторой окрестности точки (х0, у0).

Условие непрерывности f в точке х 0 можно записать в эквивалентной форме:


Теорема. Сумма, разность, произведение и частное непрерывных в точке х 0 функций f (x) и φ (x) есть непрерывная функция в этой точке, если, конечно, в случае частного φ (х 0 ) ≠ 0.
Множество G 
Говорят, что функции
Связное открытое множество называется областью.
Теорема. Пусть функция f (x) определена и непрерывна на Rn (во всех точкахRn). Тогда множество G точек х, где она удовлетворяет неравенству
f (x) > с (или f (x) 0, совпадает с G. Пусть х 0 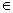
| х – х 0 | 0, т.е. он принадлежит к G и точка х 0 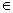
Решение. Функция z = ln (x 2 + y 2 ) терпит разрыв в точке х = 0, у = 0. Следовательно, точка О (0, 0) является точкой разрыва.
Предел функции многих переменных
Предел функции в точке.
Напомним, что окрестностью \(O(x^0)\) точки \(x^0\) в метрическом пространстве \(X\) называется любое множество, для которого точка \(x^0\) является внутренней. Проколотая окрестность \(\dot
Будем рассматривать функции \(f: \ M\rightarrow R\), где \(M\) есть некоторое множество, принадлежащее метрическому пространству \(X\). Если \(X=R^n\), то функция \(f: \ M\rightarrow R\) называется функцией многих переменных и обозначается обычно следующим образом:
$$
f(x)=f(x_1,\ldots,x_n),\quad x\in M.\nonumber
$$
Например, функция \(\displaystyle \sqrt<1-x_1^2-x_2^2>\) определена в единичном круге пространства \(R^2\) с центром в точке \((0,0)\), а функция \(\operatorname
Пусть функция \(f(x)\) определена в проколотой окрестности \(\dot
Говорят, что функция \(f(x)\), определенная в \(\dot
Эквивалентность двух определений предела доказывается так же, как и для функций одной переменной.
Если число \(A\) есть предел функции \(f(x)\) при \(x\rightarrow x_0\), то будем писать
$$
A=\lim_
$$
Если функция двух переменных \(f(x,y)\) определена в \(\dot
$$
A=\lim_
$$
и называют иногда число \(A\) двойным пределом.
Аналогично, для функции \(n\) переменных наряду с обозначением \(A=\displaystyle\lim_
$$
A=\lim_
$$
Пусть функции \(f(x)\) и \(\varphi(x)\) определены в \(\dot
\(\circ\) Так как \(\displaystyle\lim_
\(\triangle\) Возьмем любое \(\varepsilon > 0\). Положим \(\delta=\varepsilon^<1>\). Пусть \((x,y)\in S_\delta(0, 0)\), тогда
$$
(x^2+y^2)^a Пример 2.
В силу примера выше \(\displaystyle\lim_
$$
\lim_
$$
Что и требовалось доказать. \(\blacktriangle\)
\(\triangle\) Рассмотрим последовательность точек \((x_n,y_n)=\displaystyle\left(\frac<1>
Так как при любом \(n\in \mathbb
не имеет предела при \((x,y)\rightarrow (0,0)\).
\(\triangle\) Повторяя рассуждения примера 3, построим две последовательности точек \((x_n,y_n)=\displaystyle\left(\frac<1>
Предел по множеству.
Предел \(\displaystyle\lim_
Пусть \(M\) есть подмножество области определения функции \(f(x)\), \(x^0\) — предельная точка множества \(M\). Будем говорить, что число \(A\) есть предел функции \(f(x)\) по множеству \(M\) при \(x\rightarrow x^0\), если \(\forall\varepsilon > 0 \ \exists \delta > 0\) такое, что \(\forall x\in<\dot S>_\delta(x^0)\cap M\) выполнено неравенство \(|f(x)-A| Пример 5.
Показать, что предел функции \(f(x,y)=\displaystyle \frac<2xy>
\(\triangle\) Так как при \(t > 0\) выполнено равенство
$$
f(t\cos\alpha, \ t\sin\alpha)=2\sin\alpha\cos\alpha=\sin 2\alpha,\nonumber
$$
то
$$
\lim_
$$
Показать, что предел функции \(f(x,y)=\displaystyle \frac<2x^2y>
Если \(\sin\alpha=0\), то \(f(t\cos\alpha, \ t\sin\alpha)=0\) и, следовательно,
$$
\lim_
$$
Если \(\sin\alpha\neq 0\), то
$$
\lim_
$$
Ясно, что из существования \(\displaystyle\lim_
Из результатов примеров 4 и 6 следует, что из существования и равенства пределов по любому направлению в точке \((x_0,y_0)\) не вытекает существование в этой точке предела функции.
Предел функции \(f(x)\) в точке \(x^0\in R^n\) по направлению \(l=(l_1,\ldots,l_n)\), где \(l_1^2+\ldots+l_n^2=1\), определяется по аналогии со случаем функции двух переменных.
Повторные пределы. Бесконечные пределы.
Пусть функция двух переменных \(f(x,y)\) определена на множестве
$$
\Pi= <(x,y):\quad 0 0\) число \(\delta >0\), что для всех \(x\) из проколотой окрестности \(\dot
Предел и непрерывность функций нескольких переменных с примерами решения и образцами выполнения
До сих пор мы рассматривали функции одной переменной, т. е. функции, значения которых зависят от значений одной независимой переменной.
При рассмотрении многих вопросов естествознания приходится иметь дело с такими зависимостями между переменными величинами, в которых числовые значения одной из них полностью определяются значениями нескольких других. Так, например, температура тела в данный момент времени t может изменяться от точки к точке. Каждая точка тела определяется тремя координатами х, у и z, поэтому температура зависит от трех переменных х, у и z, а если еще учитывать зависимость температуры от времени t, то значения ее будут уже определяться значениями четырех переменных х, у, z и t. Площадь прямоугольника со сторонами, длины которых равны хну, определяется значениями двух переменных х и у, а объем прямоугольного параллелепипеда с ребрами, длины которых равны х, у, z, — значениями трех переменных х, у и z. Примеров таких зависимостей можно привести сколько угодно.
Эта часть курса и посвящается рассмотрению такого рода зависимостей. С этой целью вводится понятие функции нескольких переменных и развивается аппарат для исследования таких функций.
Определение функции двух и более переменных
Аналогично функции одной переменной вводится понятие функции двух переменных.
Определение:
Пусть X, Y и Z — некоторые числовые множества. Функцией двух переменных называется множество f упорядоченных троек чисел (х; у; z) таких, что 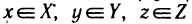
Функцию двух переменных обозначают также следующими символами: 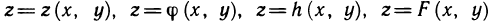
Так как каждой упорядоченной паре чисел (х; у) при фиксированной прямоугольной системе координат соответствует единственная точка М плоскости и, обратно, каждой точке М соответствует единственная упорядоченная пара чисел (х; у), то функцию двух переменных можно рассматривать как функцию точки М и вместо z=f(x; у) писать z=f(M). Областью определения функции в этом случае является некоторое множество
Способы задания функции двух переменных, как и в случае одной переменной, могут быть различными. В примерах мы используем, как правило, аналитический способ задания, когда функция задается с помощью формулы. Областью определения функции, в этом случае считается множество всех точек плоскости, для которых эта формула имеет смысл.
Примеры функций двух переменных
1. 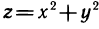
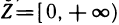
2. 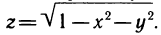
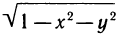
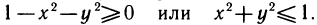
3. 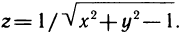
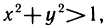
Из рассмотренных примеров следует, что областью определения функции двух переменных может быть вся плоскость Оху или ее часть.
Из аналитической геометрии известно, что множество всех упорядоченных троек чисел (х; у; z) образует координатное пространство. При этом каждой тройке (х; у; z) в пространстве соответствует точка М (х; у; z), и наоборот. Если вместо множества (М) точек плоскости взять множество 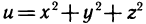
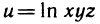
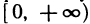
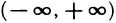
Аналогично можно дать определение функции четырех переменных u=f(x, у, z, t). В этом случае множество упорядоченных четверок чисел (х; у: z; t) образуют так называемое четырехмерное пространство, а каждая четверка (z; y; z; t) называется точкой этого пространства. Однако область определения функции четырех переменных уже не имеет наглядного геометрического истолкования. Аналогично можно ввести понятия функции пяти и вообще n переменных 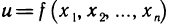
Далее подробно рассмотрены функции двух переменных; следует иметь в виду, что обобщение определений и полученных результатов на функции трех и более переменных не содержит принципиальных отличий.
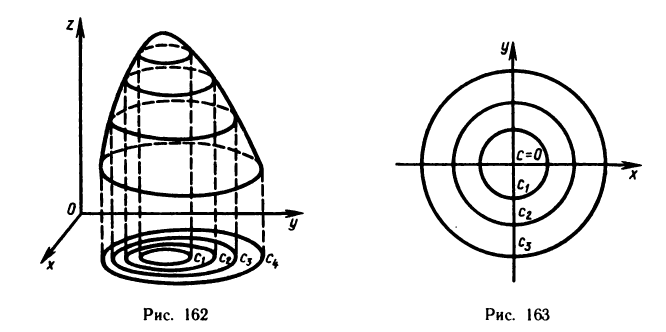
Геометрическое изображение функции двух переменных
Как известно, функция одной переменной изображается на плоскости в виде линии, определенной уравнением y=f(x). Функция двух переменных изображается в пространстве в виде поверхности, которая определяется уравнением z=f(x, у), т. е. сама формула, задающая функцию, и есть уравнение этой поверхности.
В аналитической геометрии рассматриваются различные поверхности и их уравнения. Так, например, уравнение 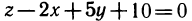
Уравнение 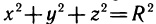
Построение графиков функций двух переменных во многих случаях представляет значительные трудности. Поэтому существует еще один способ изображения функции двух переменных, основанный на сечении поверхности z=f(x, у) плоскостями z=c, где с —любое число, т. е. плоскостями, параллельными плоскости Оху.
Назовем линией уровня функции z=f(x, у) множество точек (х; у) плоскости Оху, в которых функция принимает одно и то же значение с. Очевидно, при различных с получаются различные линии уровня для данной функции.
Если взять числа 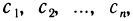
Термин «линии уровня» заимствован из картографии. Там линии уровня — это линии, на которых высота точек земной поверхности над уровнем моря постоянна. По ним можно судить не только о высоте над уровнем моря определенной точки местности, но и о характере рельефа, что особенно важно, если местность гористая.
Пример:
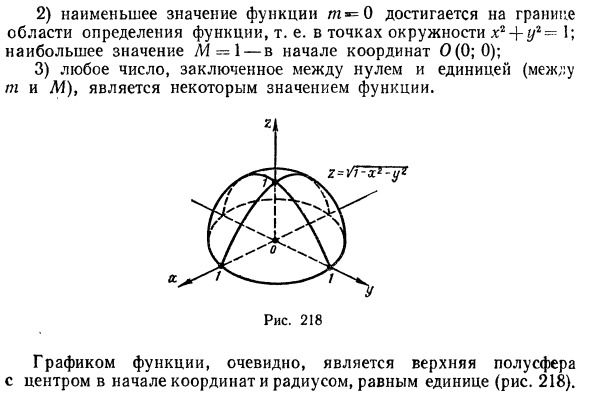
Построить линии уровня функции
Решение:
Линии уровня данной функции определяются уравнением 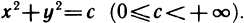
Так как в данном случае линии уровня — окружности с центрами в начале координат, то графиком данной функции должна быть поверхность вращения вокруг оси Oz. Действительно, из аналитической геометрии известно, что уравнение 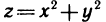
Предел функции двух переменных
Введем понятие 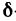
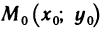
Определение:
Множество 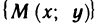
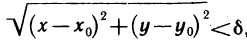
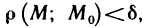
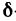
Другими словами, 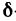
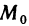
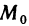
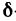
Рассмотрим последовательность точек 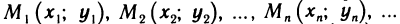
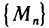
Определение:
Последовательность точек 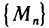
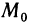

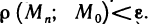
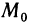
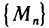
Обозначение:
Заметим, что понятие сходящейся последовательности точек плоскости является обобщением понятия сходящейся числовой последовательности. Действительно, задание последовательности 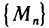
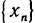
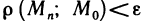
Теперь определим предел функции двух переменных. Его определение аналогично определению предела функции одной переменной.
Пусть функция z=f(M) определена на некотором множестве <М>и точка 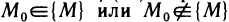
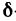
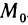
Определение:
Число А называется пределом функции z=f(М) в точке 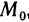
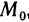
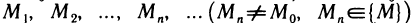
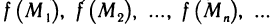
Обозначение:
Так, например, функция 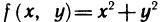
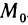
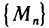
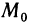
Приведем пример функции, не имеющей предела в некоторой точке. Функция 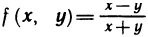
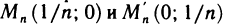
Таким образом, двум различным последовательностям точек, сходящимся к началу координат, соответствуют две последовательности значений функции, которые имеют разные пределы. Следовательно, по определению 3 данная функция не имеет предела в точке (0; 0).
Приведенное определение предела функции двух переменных дано с помощью понятия предела последовательности. Так же, как для функции одной переменной, можно дать эквивалентное определение, используя 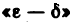
Определение:
Число А называется пределом функции z=f(AM) в точке 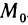

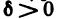
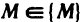
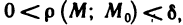
Используя логические символы, данное определение можно записать в виде
Доказательство эквивалентности определений 3 и 4 проводится точно так же, как и в случае функции одной переменной. Следует только в доказательстве теоремы 4.1 заменить последовательность 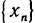
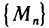
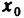
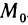
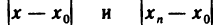
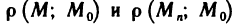
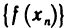
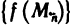
Используя определение предела функции двух переменных, можно перенести основные теоремы о пределах для функции одной переменной на функции двух переменных. Например, имеет место следующая теорема.
Теорема:
Пусть функции f(М) и g(М) определены на одном и том же множестве 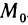
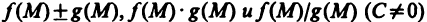
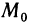
Доказательство этой теоремы аналогично доказательству теоремы 4.3 и может быть получено из него формальной заменой букв 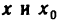
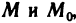
Определение:
Функция z=f(M) называется бесконечной малой в точке 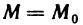
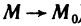
Если функция z=f(M) имеет в точке 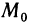
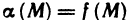
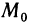
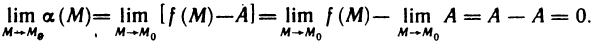
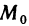
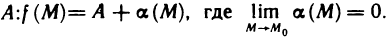

Сравнение бесконечно малых функций двух переменных производится точно так же, как и бесконечно малых функций одной переменной, причем, как и в случае одной переменной, под символом о 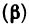
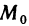

Непрерывность функции двух переменных
Понятие непрерывности функции двух переменных вводится на основе понятия предела.
Определение непрерывности функции двух переменных
Пусть на некотором множестве 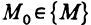
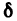

Определение:
Функция z=f(M) называется непрерывной в точке 
Согласно определению предела функции в терминах последовательностей данное определение непрерывности функции в точке 
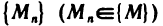
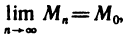
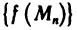
Точки, в которых функция не обладает свойством непрерывности, называются точками разрыва этой функции.
Например, функция
разрывна в точке (0; 0), так как предел этой функции при 
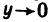
в точке (1; 2) разрывна, так как
Сформулируем определение непрерывности функции, используя определение предела функции в терминах
Определение:
Функция z=f(М) называется непрерывной в точке 

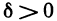
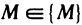
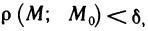
Используя символы, определение 2 можно записать в виде
Так же как для функции одной переменной, используя данные определения непрерывности и соответствующие теоремы о пределах, можно доказать, что арифметические операции над непрерывными функциями и построение сложных функций из непрерывных функций приводят к непрерывным функциям.
В дальнейшем используется определение 1 непрерывности функции, записанное в другом виде.
Назовем полным приращением функции z=f(M) в точке 
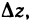
где М — любая точка из области определения функции. Пусть точки 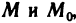
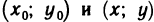
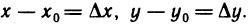
Определение 3. Функция z f (М) называется непрерывной в точке 
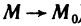
Это условие, очевидно, равносильно условию 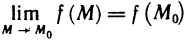
Пример:
Функция 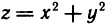
Очевидно, 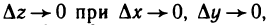
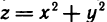
Функция z=f(М) называется непрерывной на некотором множестве <М>, если она непрерывна в каждой точке этого множества.
Основные свойства непрерывных функций двух переменных
Приведем без доказательства основные свойства непрерывных функций двух переменных, поскольку они в основном аналогичны доказательствам соответствующих свойств функций одной переменной. Предварительно введем ряд понятий для множеств <М>точек плоскости.
Определение:
Множество <М>точек плоскости называется связным, если любые две точки этого множества можно соединить непрерывной линией, состоящей из точек данного множества. Например, круг — связное множество, а множество, состоящее из двух кругов, не имеющих общих точек, не является связным.
Определение:
Точка М называется внутренней точкой множества <М>, если существует 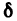
Определение:
Множество <М>, состоящее лишь из внутренних точек, называется открытым множеством.
Определение:
Связное открытое множество <М>точек называется открытой областью, или короче, областью. Простейшими областями являются: внутренность треугольника, круга, эллипса и т. п.
Определение:
Точка М называется граничной точкой области, если в любой ее 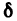
Например, для области, которая состоит из точек, лежащих внутри круга, границей является окружность.
Определение:
Множество <М>точек, образованное областью и ее границей, называется замкнутой областью.
Определение:
Множество <М>называется ограниченным, если существует круг, внутри которого оно содержится.
Отрезок и треугольник — ограниченные множества. Прямая не является ограниченным множеством.
Замкнутая ограниченная область, в которой определена функция двух переменных, является аналогом отрезка для функции одной переменной.
Теперь сформулируем основные свойства непрерывных функций двух переменных:
1°. Если функция z=f(M) непрерывна в замкнутой ограниченной области, то она ограничена в этой области, т. е. существует число k такое, что для всех точек области выполняется неравенство
2°. Если функция z=f(M) непрерывна в замкнутой ограниченной области, то она достигает в этой области своих точных граней.
3°. Если функция z=f(M) непрерывна в области, то она принимает все промежуточные значения между любыми двумя своими значениями, т. е. если 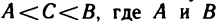

Отсюда, в частности, следует, что если 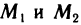
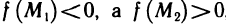

4°. Если функция z=f(M) непрерывна в замкнутой ограниченной области, то она равномерно-непрерывна в этой области, т. е. для любого 
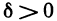
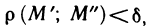
В заключение отметим, что понятия предела, непрерывности и перечисленные свойства функций двух переменных легко обобщаются на функции трех и более переменных.
Предел функции нескольких переменных. Непрерывность функции и точки разрыва









Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института