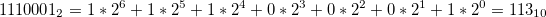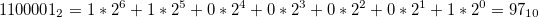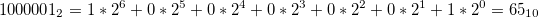Докажите что числа 1095 и 738 не являются взаимно простыми числами
Как доказать что числа 1095 и 738 не являются взаимно простыми?
Как доказать что числа 1095 и 738 не являются взаимно простыми?
При одном взгляде (для опытного глаза) или при подсчёте суммы цифр видно, что муммы цифр обоих чисел делятся на 3, значит оба числа делятся на 3. Это значит, что они не могут быть взаимно простыми.
В наборе простых множителей есть одинаковые («3»), значит эти числа имеют одинаковый множитель и не являются взаимно-простыми.
Существует общий алгоритм определения, являются ли числа взаимно простыми (он же находит наибольший общий делитель).
Алгоритм называется «Алгоритм Евклида». Его можно найти, например, в Википедии.
1095/738 = 1 и 357 в остатке
738/357 = 2 и 24 в остатке
357/24 = 14 и 21 в остатке
21/14 = 1 и 7 в остатке
17 делится на 7 без остатка, значит оба числа делятся на 7 и не являются взаимно простыми.
Перевод из двоичной системы в десятичную осуществляется по формуле:
1*2^0+0*2^1+0*2^2+ 1*2^3+1*2^4+1*2^5+1*2 ^6=1+8+16+32+64=121
Для перевода двоичного числа 1110001 в десятичную систему используем формулу:
Математическая запись этого преобразования выглядит так:
Если нужно перевести число 1100001 из двоичной системы счисления в десятичную систему можно использовать формулу:
Математическая запись этого преобразования выглядит так:
Перкеводим двоичное число 1000001 в десятичную систему по формуле:
Математически это можно записать так:
Для меня, как старого программиста, проще всего перевести 2-ное число в 16-ное, а потом в 10-ное.
Перевод из 2-го в 16-ное осуществляется очень просто.
Разбиваем число на четверки (тетрады), начиная с правого края.
Переводим каждую четверку отдельно по таблице:
0000=0; 0001=1; 0010=2; 0011=3; 0100=4; 0101=5; 0110=6; 0111=7;
1000=8; 1001=9; 1010=A; 1011=B; 1100=C; 1101=D; 1110=E; 1111=F.