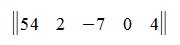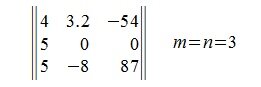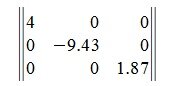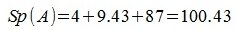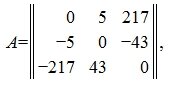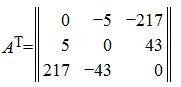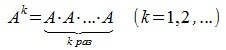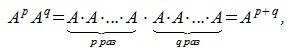Докажите что диагональные матрицы перестановочны на примере матрицы третьего порядка
Доказать утверждение о вещественной треугольной матрице

Как привести матрицу к унитреульной матрице или верхней треугольной матрице? Добавлено через 14.
Доказать утверждение
Объясните, как доказать или опровергнуть утверждение о произвольных множествах A, B, C методом.
Доказать утверждение
Подскажите, как быть с такими гипотезами, что то торможу, как аксиомы применить к такому, похоже.
Доказать утверждение
Доказать,что пересечение двух подгрупп А и В группы G будет подгруппой конечного индекса в группе.
Нет: a11^2 + a12^2 + a13^2; a22^2 + a23^2; a33^2.
Решение
Значит, матрицы A еще нет (то есть она не дана), и ее существование нужно доказать.
Диагонализируемость в данном случае не нужна, да ее и нет, как правило.
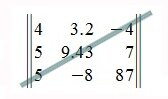
Треугольная матрица Х вычисляется из уравнения X 2 =C для треугольной же матрицы С с положительной диагональю так. Вначале вычисляем диагональные элементы из уравнений
» />
Затем, зная диагональные элементы Х и учитывая положительность диагональных элементов С, вычисляем элементы, стоящие на диагонали, параллельной главной, из формулы
» />
После этого переходим к следующей диагонали и т.д.
Рекомендую проделать все выкладки для матриц порядков 2, 3, 4. Все станет ясно.
Доказать утверждение
Докажите, что любое счетное линейно упорядоченное множество изоморфно некоторому подмножеству.
Доказать утверждение
Помогите доказать, пожалуйста:help:
Доказать утверждение
Здравствуйте. Как доказать следующее утверждение: Изоморфные графы имеют одинаковые хроматические.
Доказать утверждение
Подскажите пожалуйста как доказываются такого рода утверждения: A\subseteq B тогда и только тогда.
Матрицы. Виды матриц
Матрицей называется прямоугольная таблица из чисел с некоторым количеством m строк и с некоторым количеством n столбцов. Числа m и n называются порядками или размерами матрицы.
Матрица порядка m × n записывается в форме:
или 
Числа aij входящие в состав данной матрицы называются ее элементами. В записи aij первый индекс i означает номер строки, а второй индекс j— номер столбца.
Матрица строка
Матрица размером 1×n, т.е. состоящая из одной строки, называется матрицей-строкой. Например:
Матрица столбец
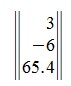
Матрица размером m×1, т.е. состоящая из одного столбца, называется матрицей-столбцом. Например
Нулевая матрица
Квадратная матрица
Матрица A порядка m×n называется квадратной матрицей, если количество строк и столбцов совпадают: m=n. Число m=n называется порядком квадратной матрицы. Например:
Главная диагональ матрицы
Побочная диагональ матрицы
Диагональная матрица
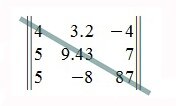
Квадратная матрица называется диагональной, если элементы, расположенные вне главной диагонали равны нулю. Пример диагональной матрицы:
Единичная матрица
След матрицы
Сумма главных диагональных элементов матрицы A называется следом матрицы и обозначается Sp A или Tr A. Например:
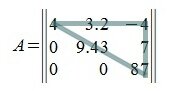
Верхняя треугольная матрица
Нижняя треугольная матрица
Квадратная матрица 
Cтолбцы матрицы A образуют пространство столбцов матрицы и обозначаются через R(A).
Ядро или нуль пространство матрицы
Противоположная матрица
Для любой матрицы A сущеcтвует противоположная матрица -A такая, что A+(-A)=0. Очевидно, что в качестве матрицы -A следует взять матрицу (-1)A, элементы которой отличаются от элементов A знаком.
Кососимметричная (Кососимметрическая) матрица
Кососимметричной называется квадратная матрица, которая отличается от своей транспонированной матрицы множителем −1:
В кососимметричной матрице любые два элемента, расположенные симметрично относительно главной диагонали отличаются друг от друга множителем −1, а диагональные элементы равны нулю.
Пример кососимметрической матрицы:
Разность матриц
Разностью C двух матриц A и B одинакового размера определяется равенством
Для обозначения разности двух матриц используется запись:
Степень матрицы
Пусть 
где E-единичная матрица.
Из сочетательного свойства умножения следует:
где p,q— произвольные целые неотрицательные числа.
Симметричная (Симметрическая) матрица
Матрица, удовлетворяющая условию A=A T называется симметричной матрицей.
Для симметричных матриц 
Доказать утверждение
В формулировке утверждения присутствуют слова «необходимо и достаточно».
Это означает, что Ваше доказательство должно состоять из двух частей:
Часть первая. НЕОБХОДИМОСТЬ.
Вы должны привести пример двух матриц A и D таких, что D — диагональная,
A — не диагональная, и матрицы A и D не перестановочны (AD не равно DA).
Часть вторая. ДОСТАТОЧНОСТЬ.
Здесь уже примерами не обойтись. Требуется рассуждение.
Нужно доказать, что ЛЮБЫЕ диагональные матрицы A и D перестановочны (AD=DA).
Небольшое уточнение.
В #4 я предполагаю, что мы заранее зафиксировали размер матриц, например, 3×3.
И это же как бы подразумевается и в старт-посте.
Но строго говоря, утверждение старт-поста должно формулироваться так:
Пусть n — произвольное натуральное число.
Для того, чтобы квадратная матрица А размера n x n была перестановочна
со всеми диагональными матрицами размера n x n, необходимо и достаточно,
чтобы матрица А сама была диагональна.
Если мы зафиксировали n, например, n=3, то в ПЕРВОЙ ЧАСТИ доказательства
(НЕОБХОДИМОСТЬ) можно привести один какой-нибудь пример двух матриц A и D
размера 3×3 таких, что D — диагональная, A — не диагональная,
и матрицы A и D не перестановочны (AD не равно DA).
Но если мы не зафиксировали n, то одного примера не достаточно.
Необходимо некоторое рассуждение, показывающее, что при любом n
такой пример существует.
Вы не понимаете, что такое НЕОБХОДИМОСТЬ.
Пока был пост №4 — я думал, что Вы описались, и не стал комментировать. Но потом появился пост №7, дублирующий Ваши грубейшие заблуждения.
То, что Вы предлагаете, НЕОБХОДИМОСТЬ не доказывает даже близко.
Решение матриц методы решений и примеров для чайников, формулы вычислений и действий с матрицами
В высшей математике существует понятие матрицы системы чисел. С комбинацией элементов, заключённых в таблице, выполняют различные операции. Прежде чем переходить к решению матриц сложными методами, следует ознакомиться с понятием этого выражения и простейшими логическими операциями над ним.
Понятие выражения
Определение гласит, что матрица — это прямоугольная таблица с заключёнными в ней числами. Её название обозначается латинскими прописными буквами (А, В). Таблицы бывают разной размерности — прямоугольной, квадратной, а также в виде строк и столбцов.
От количества строк и столбцов будет зависеть величина таблицы. Матрица размера m*n означает, что в таблице содержится m строк и n столбцов. Допустим, первая строка включает элементы а11, а12, а13, вторая — а21, а22, а23. Тогда элементы, где i = j (а11, а22) образовывают диагональ и называются диагональными.
Различают комплексные матрицы, у которых хотя бы один элемент равен комплексному числу, и действительные, когда все её элементы являются действительными числами. В математике комплексные числа представлены в виде a+b*i, где:
На приведенном примере показаны варианты.
Простейшие действия с матрицами могут быть разными. К их числу относятся:
Сложение и вычитание
Действия по сложению возможны только тогда, когда матрицы одинакового порядка равны между собой. В итоге получится новое матричное выражение такой же размерности. Сложение и вычитание выполняются по общей схеме — над соответствующими элементами таблиц проводят необходимые операции. Например, нужно сложить две матрицы А и В размерности 2*2.
Каждый элемент первой строки складывается по порядку с показателями верхней строчки второй матрицы. По аналогии производится вычитание, только вместо плюса ставится минус.
Умножение на число
Любую таблицу чисел можно умножить на число. Тогда каждый её элемент перемножается с этим показателем. К примеру, умножим матричное выражение на 2:
Операция перемножения
Матрицы подлежат перемножению одна на другую, когда количество столбцов первой таблицы равно числу строк второй. Каждый элемент Aij будет равняться сумме произведений элементов i-строки первой таблицы, перемноженных на числа в j-столбце второй. Способ произведения наглядно представлен на примере.
Возведение в степень
Формулу возведения в степень применяют только для квадратных матричных выражений. При этом степень должна быть натуральной. Формула возведения следующая:
Иначе, чтобы выполнить операцию возведения таблицы чисел в степень n, требуется умножить её на себя саму n раз. Для операции возведения в степень удобно применять свойство в соответствии с формулой:
Решение представлено на примере. 1 этап: необходимо возвести в степень, где n = 2.
2 этап: сначала возводят в степень n =2. Согласно формуле перемножают таблицу чисел саму на себя n = 2 раз.
3 этап: в итоге получаем:
Расчёт определителя
В линейной алгебре существует понятие определителя или детерминанта. Это число, которое ставят в соответствие каждой квадратной матрице, вычисленное из её элементов по специальной формуле. Определитель или модуль используется для решения большинства задач. Детерминант самой простой матрицы определяется с помощью вычитания перемноженных элементов из побочной диагонали и главной.
Определителем матрицы А n-энного порядка называется число, которое получают из алгебраической суммы n! слагаемых, попадающих под определённые критерии. Эти слагаемые являются произведением n-элементов, взятых единично из всех столбов и строк.
Произведения могут отличаться друг от друга составом элементов. Со знаком плюс будут включаться в сумму числа, если их индексы составляют чётную подстановку, в противоположном случае их значение меняется на минус. Определитель обозначается символом det A. Круглые скобки матричной таблицы, обрамляющие её элементы, заменяются на квадратные. Формула определителя:
Определитель первого порядка, состоящий из одного элемента, равен самому этому элементу. Детерминант матричной таблицы размером 2*2 второго порядка вычисляется путём перемножения её элементов, расположенных на главной диагонали, и вычитания из них произведения элементов, находящихся в побочной диагонали. Наглядный пример:
Для матрицы также можно найти дискриминант многочлена, отвечающий формуле:
Когда у многочлена имеются кратные корни, тогда дискриминант равен нулю.
Обратная матрица
Прежде чем переходить к понятию обратного выражения матрицы, следует рассмотреть алгоритм её транспонирования. Во время операции строки и столбцы переставляются местами. На рисунке представлен метод решения:
По аналогии обратная матрица сходна с обратными числами. Например, противоположной цифре 5 будет дробь 1/5 = 5 (-1) степени. Произведение этих чисел равно 1, выглядит оно так: 5*5 (-1) = 1. Умножение обычной матричной таблицы на обратную даст в итоге единичную: А* А (-1) = Е. Это аналог числовой единицы.
Но для начала нужно понять алгоритм вычисления обратной матрицы. Для этого находят её определитель. Разработано два метода решения: с помощью элементарных преобразований или алгебраических дополнений.
Более простой способ решения — путём алгебраических дополнений. Рассмотрим матричную таблицу А, обратная ей А (-1) степени находится по формуле:
Матрица обратного вида возможна только для квадратного размера таблиц 2*2, 3*3 и т. д. Обозначается она надстроенным индексом (-1). Задачу легче рассмотреть на более простом примере, когда размер таблицы равен 2*2. На первом этапе выполняют действия:
2 этап: рассчитывают матрицу миноров, которая имеет те же значения, что и первоначальная. Под минором k-того порядка понимается определитель квадратной матрицы порядка k*k, составленный из её элементов, которые располагаются в выбранных k- столбцах и k-строках.
При этом расположение элементов таблицы не меняется. Чтобы найти минор верхнего левого числа, вычёркивают строчку и столбец, в которых прописан этот элемент. Оставшееся число и будет являться минором. На выходе должна получиться таблица:
3 этап: находят алгебраические дополнения.
4 этап: определяют транспонированную матрицу.
Проверка решения: чтобы удостовериться, что обратная таблица чисел найдена верно, следует выполнить проверочную операцию.
В рассматриваемом примере получается единичная матрица, когда на главной диагонали находятся единицы, при этом другие элементы равняются нулю. Это говорит о том, что решение было найдено правильно.
Нахождение собственных векторов
Определение собственного вектора и значений матричного выражения легче понять на примере. Для этого задают матричную таблицу чисел и ненулевой вектор Х, называемый собственным для А. Пример выражения:
Согласно теореме собственными числами матричного выражения будут корни характеристического уравнения:
Из однородной системы уравнений можно определить координаты собственного вектора Х, который соответствует значению лямбда.
Метод Гаусса
Методом Гаусса называют способ преобразования системы уравнений линейного вида к упрощённой форме для дальнейшего облегчённого решения. Операции упрощения уравнений выполняют с помощью эквивалентных преобразований. К таким относят:
Чтобы понять механизм решения, следует рассмотреть линейную систему уравнений.
Следует переписать эту систему в матричный вид:
А будет являться таблицей коэффициентов системы, b — это правая часть ограничений, а Х — вектор переменных координат, который требуется найти. Для решения используют ранг матрицы. Под ним понимают наивысший порядок минора, который отличается от 0.
В этом примере rang (A) = p. Способ эквивалентных преобразований не изменяет ранг таблицы коэффициентов.
Метод Гаусса предназначен для приведения матричной таблицы коэффициентов А к ступенчатому или диагональному виду. Расширенная система выглядит так:
Обращают внимание на последние строки.
В этом случае система уравнений имеет решение, но когда хотя бы одно из этих чисел отличается от нуля, она несовместима. Таким образом, система совместима, если ранг таблицы А равен расширенному рангу В (А|b).
Если rang А=rang (A|b), то существует множество решений, где n-p — многообразие. Из этого следует n-p неизвестных Хр+1,…Xn выбираются произвольно. Неизвестные X1, X2,…Xp вычисляют следующим образом: из последнего уравнения выражают Хр через остальные переменные, вставляя в предыдущие выражения. Затем из предпоследнего уравнения получают Хр-1 через прочие переменные и подставляют их в предыдущие выражения. Процедуру повторяют.
Найти быстро ответ и проверить себя позволяет онлайн-калькулятор. Решение матрицы методом Гаусса с помощью такого расчёта показывает подробные этапы операций. Для нахождения достаточно указать количество переменных и уравнений, отметить в полях значения чисел и нажать кнопку «Вычислить».
Способ Крамера
Метод Крамера используют для решения квадратной системы уравнений, представленной в линейном виде, где определитель основной матрицы не равен нулю. Считается, что система обладает единственным решением. Например, задана система линейных уравнений:
Её необходимо заменить равноценным матричным уравнением.
Второй столбец вычисляют, а первый уже задан. Есть предположение, что определитель матрицы отличен от нуля. Из этого можно сделать выводы, что существует обратная матрица. Перемножив эквивалентное матричное уравнение на обратного формата матрицу, получим выражение:
В итоге получают выражения:
Из представленных уравнений выделяют формулы Крамера:
Метод Крамера не представляет сложности. Он может быть описан следующим алгоритмом:
Проверить решение матрицы методом Крамера онлайн позволяет калькулятор автоматического расчёта. Для получения быстрого ответа в представленные поля подставляют переменные числа и их количество. Дополнительно может потребоваться указание вычислительного метода разложения по строке или столбу. Другой вариант заключается в приведении к треугольному виду.
Указывается также представление чисел в виде целого числа, обыкновенной или десятичной дроби. После введения всех предусмотренных параметров и нажатия кнопки «Вычислить» получают готовое решение.
Описание файла
Просмотр DJVU-файла онлайн
Найти е’,Ае, если А = (а; ) е К «», а е’, и е — единичные строка и столбец подходящих размеров. 1.14. Мапгричной единицей Е, размера т х и называется матрица, у которой элемент в позиции (г, г) равен единице, а все остальные элементы равны нулю. Для произвольной матрицы А и матричной единицы Е,б подходящего размера вычислить: а) АЕеб б) Е, А. 1.15. Найти ДА): а) Д
х) = хг — 2х+ 2, А = б)
6 2) произведение А
6 Глава 1. Матрицы 1.16. Доказать, что каждая квадратная матрица второго по-
с х — (а+ а1)х+ (ай — бс) = О. 1.17. Доказать, что если А — диагональная матрица, то матрица ДА) также диагональная, каков бы ни был многочлен Дх). 1.18. Вычислить: а) ; б) — 2 — 4 0 1.19.
Вычислить а),; б) д) 1 О,п>2; е) ) О Л ‘ ) О 1 спаса — в1па 1 в1па спаса
= (А+ В)(А — В). 1.24. Доказать, что если матрицы А и В перестановочны, то: а) 4з+ Вз (4+ ВИАз 4В+ Вз). б) (А+ В) А +С,’,А22-
В + + В 1.25. Найти п-ю степень матрицы А, если матрица А равна: 6)
— 4 — 5 10 11 Аа Азв 1.26. В ычислить матрицу + + + +, если матрица А равна:
— 2 — 21′ )[ а) 2 2,’ б) 1.27. Найти все если: )А=
— 2 — 21 матрицы, перестановочные с матрицей А, б)А= 2 1, в)А= 0100 0010 0001 г) А= 0000 ) А — квадратна е я матрица и-го порядка, все элементы которой равны единице. 1.28. Доказать, что умножение матрицы А слева на диагональную матрицу 1А’ = 222а81Лц Лз. Л„) равносильно умноже- )А= [ б) А= 1010’с2 — 1о — 1’23 с2 — 1 22 ‘ — 10 — 9 д) А — матричная единица В2.
Е 222″ 22; Глава 1. Матрицы нию строк А соответственно на Лы Лз. Л„, умножение же А на Р справа равносильно аналогичному изменению столбцов. 1.29. Найти матрицу А, если И,’И 2 5 А= 1.30. Доказать, что если А — диагональная матрица и все элементы ее главной диагонали различны между собой, то любая матрица, перестановочная с А, также диагональна. 1.31. Доказать, что квадратная матрица А перестановочна со всеми диагональными матрицами тогда и только тогда, когда она сама является диагональной. 1.32.
Доказать, что квадратная матрица А перестановочна со всеми квадратными матрицами того же порядка тогда и только тогда, когда она является скалярной. 1.33. Доказать, что если матрица А перестановочна с матрицей В, то она перестановочна и с матрицей В
. Верно ли обратное? 1.34. Пусть А — квадратная матрица и 1(х) и д(х) — произвольные многочлены. Показать, что матрицы 1(А) и д(А) перестановочны.
1.35. Доказать, что след матрицы обладает следующими свойствами: а) сг(А+ В) = сгА+ сгВ; б) сг(аА) = асгА; в) сг(Ат) = сгА; г) сг(АВ) = сг(ВА), если произведения АВ, ВА определены. 1.36. Доказать, что для любой матрицы величина Сг(АтА) неотрицательна, причем равна нулю тогда и только тогда, когда матрица А нулевая. 1.36.1. Существуют ли матрицы А и В, для которых равенство АХВ = Х
выполняется при любой матрице Х б К
«»? 1.36.2. Можно ли свести операцию транспонирования матрицы общего вида к операциям умножения ее слева и справа на какие-либо наперед заданные матрицы? 1.37.
Доказать, что для любых квадратных матриц А и В одинакового размера их коммутатор [А, В] имеет нулевой след. 1.38. Доказать, что равенство [А, В] = 1 не выполнено ни для каких вещественных матриц А и В. 19 з1. Операции над матрицами и [аб) Е К'»»» величина т, =
си 1=1 т суммой, а величина с =
=1 1.39. Для матрицы А = называется ее г-й стпрочной
-й столбцовой суммой. а) Показать, что т
Считая, что произведение АВ определено, доказать, что все строчные суммы в АВ также одинаковы и равны ар’. в) Сформулировать и доказать столбцовый вариант утверждения пункта «б». 1.40. Доказать, что если квадратные матрицы А и В порядка и таковы, что для любого вектор-столбца С Е К»»
выполнено соотношение Ас = Вс, то А = В. 1.41.
Доказать, что если квадратные матрицы А и В порядка и таковы, что для любых вектор-столбцов С, и Е К»»» выполнено соотношение с,
Ви, то А = В. 1.42. Найти коммутатор матричных единиц Е, и Еы и показать, что он нулевой тогда и только тогда, когда либо г = у = 1с = 1, либо [1 — 1с) [1 — 1) ф О. 1.43. Доказать, что диагональная матрица с нулевым следом является линейной комбинацией коммутаторов матричных единиц. 1.44. Показать, что коммутатор обладает следующими свойствами: Глава 1, Матрицы 20 1.45. Доказать,что равенство [[А, В],С] = [А, [В,С)] выполнено тогда и только тогда, когда матрицы [А, С] и В пере- становочны.
1.46. Доказать, что для любых матриц А, В, С второго по- рядка выполнено соотношение [[[А, В]) г, С] = О. 1.47. Доказать, что любая матрица с нулевым следом явля- ется суммой коммутаторов матриц с нулевым следом. 1.48. Доказать, что для любой матрицы А с нулевой глав- ной диагональю найдутся матрица Х и диагональная матрица Р такая, что [Х, Р) = А. 1.49. Произведениелл Йордана А в В квадратных матриц А и В одного порядка называется матрица 1[АВ + ВА). Показать, что произведение Иордана обладает следующими свойствами: а) А*В = В в А; б) [сгА) в В = сгА * В; в) [А+В) е С= А*С+В*С; г) А*А = Аг; д) А*1=А; В)т Ат „Вт, ж) [Аг в В) * А = Аг * [В* А), выполненными для любых квадратных матриц А, В, С и еди- ничной матрицы 1 одного порядка.
2.2. Найти количество операций умножения, необходимых для вычисления произведения двух треугольных матриц порядка и одного вида. 2.3. Пусть А = (а,у) — треугольная матрица и-го порядка и »с Е (Ч. Найти йг А». 2.4. Доказать, что для любой треугольной матрицы А с положительными диагональными элементами найдется треугольная матрица В того же вида с положительными диагональными элементами такая, что В
, то произведению АВ соответствует блочная матрица С = (Сс ) с элементами з Ссс =
АссВсг. с=с 2.8. Применяя описанное в предыдущей задаче правило умножения блочных матриц, вычислить й— ‘[4— б) [ — 1 — 1 — 2 — 1 0 0 100 011 001 — 2 в)012 110 1;г)202 — 110 ной.
2.6. Квадратная матрица А порядка п.называется ленпсочной, если для некоторого числа т (меньшего и — 1) все элементы а; с индексами, удовлетворяющими условию
с — Я ) т, равны нулю. Число 2т+ 1 называется шириной ленты. Найти ширину ленты произведения ленточных матриц, если для сомножителей эта ширина равна 2псс + 1, 2тг + 1 соответственно и тс + тг