Докажите что осевое сечение цилиндра является прямоугольником две противоположные стороны которого
Урок «Понятие цилиндра»
Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Введем понятие цилиндра – геометрического тела.
Ну конечно, все вы видели много предметов в быту, похожих на данное тело.
Все прямые образуют поверхность, которая называется цилиндрической.
Каждая из этих прямых называется образующей цилиндрическую поверхность, а прямая, проходящая через центр окружности, – осью цилиндрической поверхности.
Далее проведем плоскость сигма, параллельную плоскости альфа, таким образом, что они отделят отрезки образующих, которые равны и параллельны между собой.
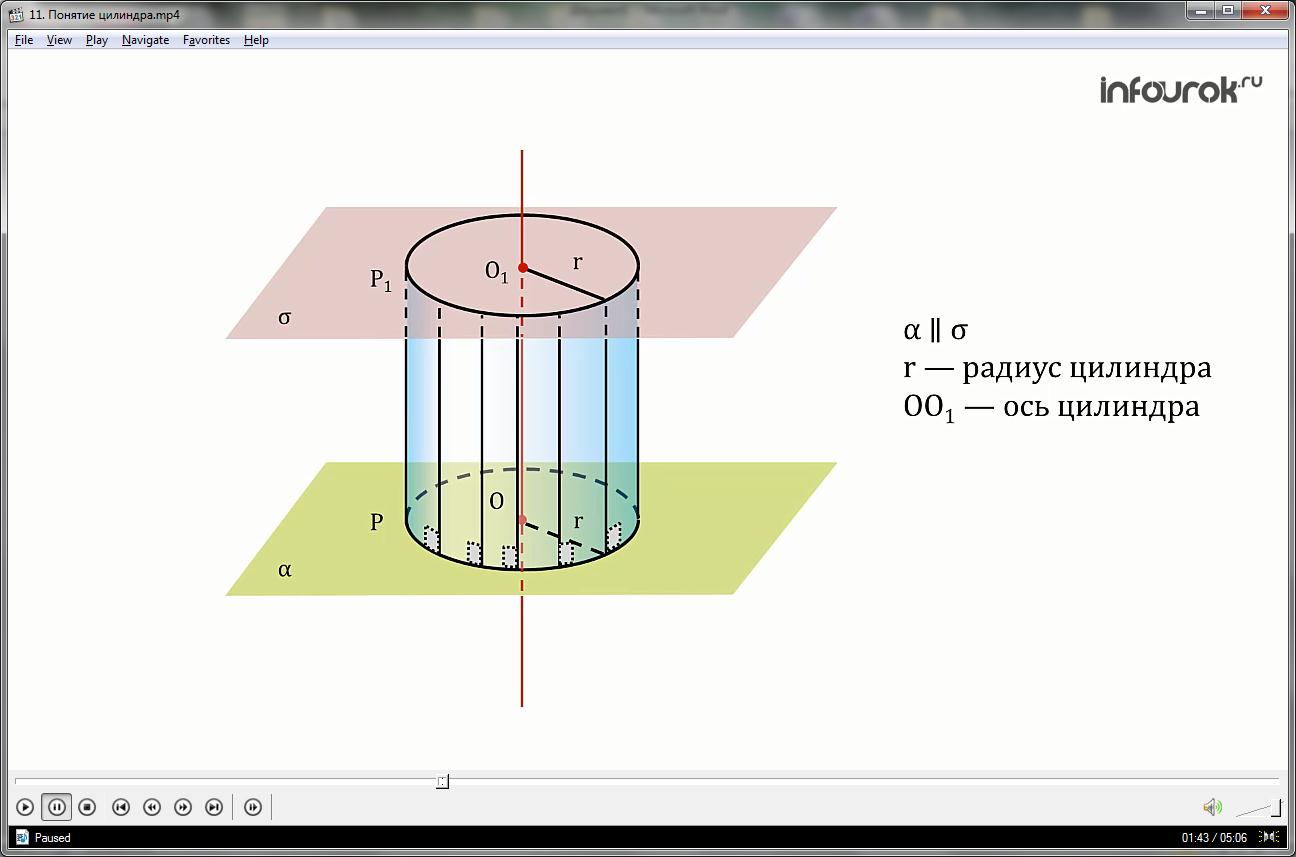
Ось цилиндрической поверхности пройдет через центр О1 окружности Р1, радиус окружностей будет равный r. Таким образом, мы получили цилиндр.
Цилиндром называется тело, ограниченное цилиндрической поверхностью и двумя кругами, лежащими в параллельных плоскостях.
Ось ОО1 – называют осью цилиндра, отрезок образующей цилиндрической поверхности ТТ1– образующая цилиндра.
Цилиндрическая поверхность, т.е. поверхность, составленная из образующих, называется боковой поверхностью цилиндра, а круги – основаниями цилиндра.
Длина образующей называется высотой цилиндра, а радиус основания — радиусом цилиндра.
Цилиндр может быть получен вращением прямоугольника вокруг одной из его сторон. На рисунке изображен цилиндр, полученный вращением прямоугольника вокруг стороны ОО1.
Рассмотрим сечение цилиндра.
1) Если секущая плоскость проходит через ось цилиндра, то сечение представляет собой прямоугольник, две стороны которого – образующие, а две другие – диаметры оснований цилиндра. Такое сечение называется осевым.
2) Если секущая плоскость перпендикулярна оси цилиндра, то сечение является кругом.
Теперь давайте посмотрим, какие бывают цилиндры.
1) Прямые и наклонные, в зависимости от того, перпендикулярны или наклонны плоскости оснований к образующим.
2) Сложные цилиндры.
изображён цилиндр, каждое основание которого представляет собой фигуру, ограниченную частью параболы и отрезком.
На втором рисунке изображен цилиндр, основаниями которого являются круги, но образующие цилиндра не перпендикулярны к плоскости оснований (наклонный цилиндр).
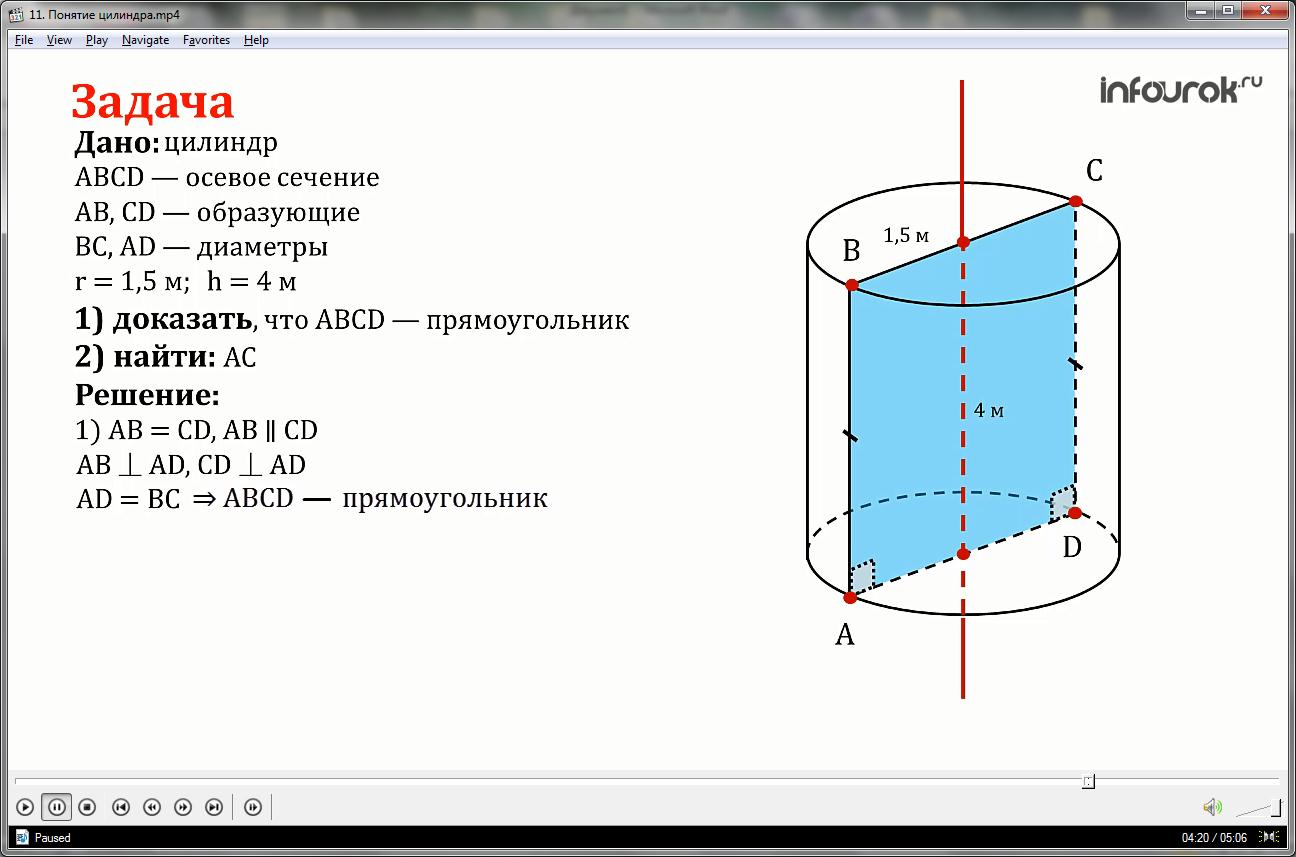
Докажите, что осевое сечение цилиндра является прямоугольником, две противоположные стороны которого – образующие, а две другие – диаметры оснований цилиндра. Найти диагональ осевого сечения, если радиус цилиндра равен 1,5 м, а высота равна 4 м.
1) так как АВ и CD – образующие то они равны и параллельны, и по определению образующих цилиндра АВ и CD перпендикулярны основанию.
AD и BC равны как диаметры оснований,
следовательно, четырехугольник ABCD по признаку параллелограмма и определению является прямоугольником.
2) Диагональ АС делит прямоугольник на два равных прямоугольных треугольника, тогда,
из прямоугольного треугольника АВС находим АС: по теореме Пифагора АС равна корню квадратному из суммы квадратов сторон АВ и АС, где АВ равна высоте цилиндра, а ВС диаметру основания то есть двум радиусам.
Урок «Понятие цилиндра»
Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Введем понятие цилиндра – геометрического тела.
Ну конечно, все вы видели много предметов в быту, похожих на данное тело.
Все прямые образуют поверхность, которая называется цилиндрической.
Каждая из этих прямых называется образующей цилиндрическую поверхность, а прямая, проходящая через центр окружности, – осью цилиндрической поверхности.
Далее проведем плоскость сигма, параллельную плоскости альфа, таким образом, что они отделят отрезки образующих, которые равны и параллельны между собой.
Ось цилиндрической поверхности пройдет через центр О1 окружности Р1, радиус окружностей будет равный r. Таким образом, мы получили цилиндр.
Цилиндром называется тело, ограниченное цилиндрической поверхностью и двумя кругами, лежащими в параллельных плоскостях.
Ось ОО1 – называют осью цилиндра, отрезок образующей цилиндрической поверхности ТТ1– образующая цилиндра.
Цилиндрическая поверхность, т.е. поверхность, составленная из образующих, называется боковой поверхностью цилиндра, а круги – основаниями цилиндра.
Длина образующей называется высотой цилиндра, а радиус основания — радиусом цилиндра.
Цилиндр может быть получен вращением прямоугольника вокруг одной из его сторон. На рисунке изображен цилиндр, полученный вращением прямоугольника вокруг стороны ОО1.
Рассмотрим сечение цилиндра.
1) Если секущая плоскость проходит через ось цилиндра, то сечение представляет собой прямоугольник, две стороны которого – образующие, а две другие – диаметры оснований цилиндра. Такое сечение называется осевым.
2) Если секущая плоскость перпендикулярна оси цилиндра, то сечение является кругом.
Теперь давайте посмотрим, какие бывают цилиндры.
1) Прямые и наклонные, в зависимости от того, перпендикулярны или наклонны плоскости оснований к образующим.
2) Сложные цилиндры.
изображён цилиндр, каждое основание которого представляет собой фигуру, ограниченную частью параболы и отрезком.
На втором рисунке изображен цилиндр, основаниями которого являются круги, но образующие цилиндра не перпендикулярны к плоскости оснований (наклонный цилиндр).
Докажите, что осевое сечение цилиндра является прямоугольником, две противоположные стороны которого – образующие, а две другие – диаметры оснований цилиндра. Найти диагональ осевого сечения, если радиус цилиндра равен 1,5 м, а высота равна 4 м.
1) так как АВ и CD – образующие то они равны и параллельны, и по определению образующих цилиндра АВ и CD перпендикулярны основанию.
AD и BC равны как диаметры оснований,
следовательно, четырехугольник ABCD по признаку параллелограмма и определению является прямоугольником.
2) Диагональ АС делит прямоугольник на два равных прямоугольных треугольника, тогда,
из прямоугольного треугольника АВС находим АС: по теореме Пифагора АС равна корню квадратному из суммы квадратов сторон АВ и АС, где АВ равна высоте цилиндра, а ВС диаметру основания то есть двум радиусам.
№521. Докажите, что осевое сечение цилиндра является прямоугольником, две противоположные
Задание №521 — ГДЗ по геометрии 11 класс (Атанасян Л.С.)Подробнее
Задание №522 — ГДЗ по геометрии 11 класс (Атанасян Л.С.)Подробнее
Задание №531 — ГДЗ по геометрии 11 класс (Атанасян Л.С.)Подробнее
Задание №524 — ГДЗ по геометрии 11 класс (Атанасян Л.С.)Подробнее
Задание №535 — ГДЗ по геометрии 11 класс (Атанасян Л.С.)Подробнее
№522. Диагональ осевого сечения цилиндра равна 48 см. Угол между этой диагональю и образующейПодробнее
осевое сечение цилиндраПодробнее
№531. Высота цилиндра равна 10 дм. Площадь сечения цилиндра плоскостью, параллельнойПодробнее
11 класс, 14 урок, Понятие цилиндраПодробнее
№525. Площадь осевого сечения цилиндра равна 10 м2, а площадь основания — 5 м2.Подробнее
ЕГЭ Задание 14 Сечение цилиндраПодробнее
Задание №537 — ГДЗ по геометрии 11 класс (Атанасян Л.С.)Подробнее
РЕШЕНИЕ ЗАДАЧ НА ЦИЛИНДРПодробнее
№533. Высота цилиндра равна h, а площадь осевого сечения равна 5. Найдите площадь сеченияПодробнее
Конспект лекции (раздаточный материал) по учебной дисциплине «Математика: геометрия» по разделу » Цилиндр, конус, шар»
Выбранный для просмотра документ Конспект лекций Цилиндр, конус,шар.docx
МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
«ВОЛЖСКИЙ ИНСТИТУТ ЭКОНОМИКИ, ПЕДАГОГИКИ И ПРАВА»
Волжский социально-педагогический колледж
Математика:Геометрия (10-11кл., 1 курс СПО)
Конспект лекций (раздаточный материал) по разделу
Автор: Бондаренко Людмила Валентиновна
Место работы: Волжский социально-педагогический колледж – структурное подразделение ВИЭПП
Как уже отмечалось, все образующие цилиндра параллельны и равны друг другу. Длина образующей называется высотой цилиндра, а радиус основания — радиусом цилиндра.
Площадь поверхности цилиндра
За площадь боковой поверхности цилиндра принимается площадь ее развертки.
Решение задач по теме « Цилиндр»
521. Докажите, что осевое сечение цилиндра является прямоугольником, две противоположные стороны которого — образующие, а две другие — диаметры оснований цилиндра. Найдите диагональ осевого сечения, если радиус цилиндра равен 1,5 м, а высота 4м.
522. Диагональ осевого сечения цилиндра равна 48 см. Угол между этой диагональю и образующей цилиндра равен 60°. Найдите: а) высоту цилиндра; б) радиус цилиндра; в) площадь основания цилиндра
523. Осевое сечение цилиндра — квадрат, диагональ которого равна 20 см. Найдите: а) высоту цилиндра; б) площадь основания цилиндра.
531. Высота цилиндра равна 10 дм. Площадь сечения цилиндра плоскостью, параллельной оси цилиндра и удаленной на 9 дм от нее, равна 240 дм 2 Найдите радиус цилиндра
545. Цилиндр получен вращением квадрата со стороной а вокруг одной из его сторон. Найдите площадь: а) осевого сечения цилиндра; б) боковой поверхности цилиндра; в) полной поверхности цилиндра.
Тело, ограниченное конической поверхностью и кругом с границей L, называется конусом (рис. 149). Круг называется основанием конуса, вершина конической поверхности — вершиной конуса, отрезки образующих, заключенные между вершиной и основанием, — образующими конуса, а образованная ими часть конической поверхности — боковой поверхностью конуса. Ось конической поверхности называется осью конуса, а ее отрезок, заключенный между вершиной и основанием, — высотой конуса. Отметим, что все образующие конуса равны друг другу (объясните почему).
Конус может быть получен вращением прямоугольного треугольника вокруг одного из его катетов. На рисунке 150 изображен конус, полученный вращением прямоугольного треугольника ABC вокруг катета АВ . При этом боковая поверхность конуса образуется вращением гипотенузы АС , а основание — вращением катета ВС .
Площадь поверхности конуса
Таким образом, площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую.
Площадью полной поверхности конуса называется сумма площадей боковой поверхности и основания. Для вычисления площади S кон полной поверхности конуса получается формула
Часть конической поверхности, ограничивающая усеченный конус, называется его боковой поверхностью, а отрезки образующих конической поверхности, заключенные между основаниями, называются образующими усеченного конуса. Все образующие усеченного конуса равны друг другу (докажите это самостоятельно).
547. Высота конуса равна 15 см, а радиус основания равен 8 см. Найдите образующую конуса.
550. Осевое сечение конуса — прямоугольный треугольник. Найдите площадь этого сечения, если радиус основания конуса равен 5 см.
555. Высота конуса равна 10 см. Найдите площадь сечения, проходящего через вершину конуса и хорду основания, стягивающую дугу в 60°, если плоскость сечения образует с плоскостью основания конуса угол: а) 30°; б) 45°; в) 60°.
Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки (рис. 157).
Тело, ограниченное сферой, называется шаром. Центр, радиус и диаметр сферы называются также центром, радиусом и диаметром шара. Очевидно, шар радиуса R с центром О содержит все точки пространства , которые расположены от точки О на расстоянии, не превышающем R (включая и точку О), и не содержит других точек.
Взаимное расположение сферы и плоскости
Касательная плоскость к сфере
Рассмотрим более подробно случай, когда сфера и плоскость имеют только одну общую точку.
Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка называется точкой касания плоскости и сферы.
Радиус сферы, проведенный в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.
Обратная теорема . Если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащий на сфере, то эта плоскость является касательной к сфере. (Самостоятельно)
Формула для вычисления площади сферы радиуса R: S = 4π г 2