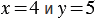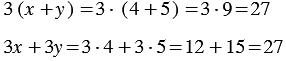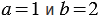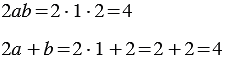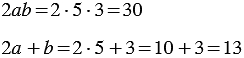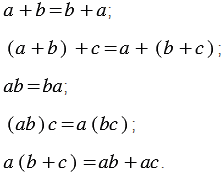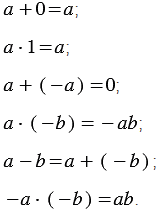Докажите что равенство не является тождеством х2 х7 х14
Тождество. Тождественные преобразования. Примеры.
Тождества в основном применяются для решения линейных уравнений.
Тождеством называется равенство, которое верно при всех значениях переменных.
Или другими словами, тождество — это равенство, которое выполняется на всём множестве значений переменных, входящих в него, например:
В этих выражениях при всех значениях a и b равенство верное.
2 выражения с равными значениями при всех значениях переменных являются тождественно равными.
Равенство x+2=5 может существовать не при всех значениях x, а лишь при x=3. Это равенство не будет тождеством, это будет уравнением. Кроме того, тождеством будет равенство, которое не содержит переменные, например 25 2 =625.
Тождественное равенство обозначают символом «≡» (тройное равенство).
Примеры тождеств.
— Тождество Эйлера (кватернионы);
— Тождество Эйлера (теория чисел);
— Тождество четырёх квадратов;
— Тождество восьми квадратов;
Тождественные преобразования.
Тождественное преобразование выражения (преобразование выражения) – это подмена одних выражений другими, тождественно равными друг другу.
Для тождественных преобразований используют формулы сокращенного умножения, законы арифметики и другие тождества.
Выполним тождественные преобразования с такой дробью: 
.
Полученное тождество, при х ≠ 0 и х ≠ 1 (недопустимые значения), т.к. знаменатель левой части не может быть равен нулю.
Доказательство тождеств.
Для того, чтоб доказать тождество нужно сделать тождественные преобразования обеих или одной части равенства, и получить слева и справа одинаковые алгебраические выражения.
Например, доказать тождество:
Вынесем х за скобки:
Это равенство есть тождество, при х≠0 и х≠1.
Чтоб доказать, что равенство не является тождеством, нужно найти 1-но значение переменной (которое допустимо) у которой числовые выражения (которые были получены) станут не равными друг другу.
5−1 ≠ 5+1 — подставим, к примеру, 5.
Это равенство не тождество.
Разница между тождеством и уравнением.
Тождество верно при всех значениях переменных, а уравнение – это равенство, которое верно только при одном либо нескольких значениях переменной.
Это выражение верно лишь при х = 10.
Тождеством будет равенство, которое не содержит переменных.
Тождественно равные выражения. Тождества
| Два выражения, значения которых равны при любых значениях переменных, называют тождественно равными. |
Рассмотрим две пары выражений:
1) 
и 
Найдем их значения при 
Мы получили один и тот же результат. Из распределительного свойства следует, что вообще при любых значениях переменных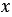 
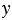
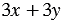
и 
значения выражений и равны.
2) 
Найдем их значения при 
Мы получили один и тот же результат. Однако, можно указать такие значения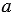 
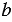
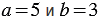
и 
, при которых значения этих выражений не будут иметь равные значения. Например, если 
, то
Мы получили разные результаты.
Следовательно, выражения и являются тождественно равными, а выражения не являются тождественно равными.
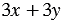
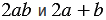
| Равенство, верное при любых значениях переменных, называется тождеством. |
Равенство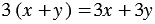 
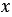
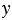
— тождество, т.к. оно верно при любых значениях и .
Также к тождествам можно отнести равенства, выражающие свойства сложения и умножения чисел:
Можно привести и другие примеры тождеств:
Тождествами считают и верные числовые равенства.
Очень часто при вычислении значений выражений, легче сначала упростить имеющееся выражение, а затем выполнять вычисления.
| Замену одного выражения другим, тождественно равным ему выражением, называют тождественным преобразованием или просто преобразованием выражения. |
К тождественным преобразованиям можно отнести приведение подобных слагаемых и раскрытие скобок.
Примеры:
1) 
, мы преобразовали выражение 
в выражение 
.
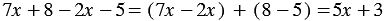
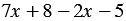
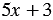
2) 
, мы преобразовали выражение 
в выражение 
.
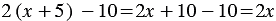
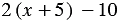
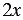
Для того, чтобы доказать, что данное равенство является тождеством (или доказать тождество), используют следующие методы:
1) тождественно преобразуют одну из частей данного равенства, получая другую часть;
2) тождественно преобразуют каждую из частей данного равенства, получая одно и то же выражение;
3) доказывают, что разность левой и правой частей данного равенства тождественно равна нулю.
Также, чтобы доказать, что равенство не является тождеством, достаточно привести контрпример, т.е. указать такое значение переменной (или переменных, если их несколько), при котором данное равенство не выполняется.
Пример: Докажите, что равенство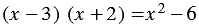 
не является тождеством.
Решение: Приведем контрпример. Если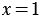 
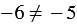
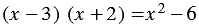
, то
, следовательно, равенство не является тождеством.
Поделись с друзьями в социальных сетях:
С-06 Тождества (Алгебра 7)
С-06 Тождества (Алгебра 7)
Самостоятельная работа № 6 по алгебре в 7 классе «Тождественно равные выражения. Тождества» с ответами. Дидактические материалы (упражнения №№ 17 — 23) для учителей, учащихся и родителей. С-06 Тождества (УМК Мерзляк).
Алгебра 7 класс (Мерзляк)
Самостоятельная работа № 6 «Тождества»
С-06. Вариант 1
С-06. Вариант 2
С-06. Вариант 3
Алгебра 7 Мерзляк С-06 Тождества.
ОТВЕТЫ на самостоятельную работу:
Ответы на Вариант 1 :
№ 44. –7а – b. Ответ: 3.
№ 45. 1)–5а + 20; 2) 3b + 33; 3)–2с;
№ 46. 1) (а – 1) 2 ≠ а 2 – 1, потому что а 2 – 2а + 1 ≠ а 2 – 1;
2) (с – 2)(с + 3) ≠ (с – 2) • с + 3, так как с 2 + с – 6 ≠ с 2 – 2с + 3.
Ответы на Вариант 2 :
№ 44. –6m + n. Ответ: 3.
№ 45. 1) 6х – 10; 2) –2у – 12; 3) –5z.
№ 46. 1) а 3 + 6а 2 + 12а + 8 ≠ а 3 + 8; 2) х 2 – 9 ≠ 4х – 9
Ответы на Вариант 3 :
№ 44. – с – 14d. Ответ: 4.
№ 45. 1) m + 9; 2) 26 – 10n; 3) –3р.
№ 46. 1) 16 + 8р + р 2 ≠ 16 + р 2 ; 2) (а + 4)(а + 5) = а 2 + 9а + 20 ≠ а 2 + 20.
Вы смотрели: Самостоятельная работа С-06 Тождества по алгебре в 7 классе «Тождественно равные выражения. Тождества» с ответами. Дидактические материалы для учителей, учащихся и родителей.
Цитаты (упражнения) из учебного пособия «Дидактические материалы. Алгебра 7 класс / Мерзляк, Полонский, Рабинович, Якир — М.:Вентана-Граф» использованы на сайте исключительно в учебных целях (пп. 1 п. 1 ст. 1274 ГК РФ). Решения и ОТВЕТЫ на самостоятельную работу (нет в пособии) адресованы родителям для проверки знаний учащихся.
Конспект урока «Доказательство тождеств».
Конспект урока «Доказательство тождеств».
Тема урока: Доказательство тождеств.
Тип урока: Урок изучения нового материала.
научить использовать способы преобразования многочленов для доказательства тождеств. Рассмотреть способы доказательства тождеств, способствовать выработке навыков доказательства тождеств. Проверить усвоение учащимися пройденного материала, сформировывать умения применения изученного
Планируемые результаты обучения:
— смыслообразования (осознание личностного смысла учебной деятельности, формирование внутренней мотивации к учению в связи с интересами и жизненными планами ученика)
— положительное отношение к учению, к познавательной деятельности,
— рефлексия собственной деятельности,
Знать: определение тождества; способы доказательства тождеств;
Понимать: в чем отличие тождества от других равенств;
Уметь: доказывать тождества различными способами: способом преобразования одной части к виду другой, способом одновременного преобразования обеих частей к тождественно равным выражениям, с помощью доказательства равенства нулю разности частей тождества.
-постановка учебной задачи на основе соотнесения того, что уже известно и усвоено учащимся, и того, что еще неизвестно,
-выбор, принятие и сохранение учебной цели и задачи,
— осуществление самоконтроля и самооценки, осознание качества и уровня усвоения,
— умение определить способы действий, алгоритм решения задачи в рамках предложенных условий и требований,
— умение оценивать правильность выполнения учебной задачи, собственные возможности её решения,
— умение создавать, применять и преобразовывать знаки и символы, алгоритмы и схемы для решения учебных и познавательных задач,
— самостоятельное выделение и формулирование познавательной цели; поиск и выделение необходимой информации, применение методов информационного поиска,
— умение структурировать знания; умение осознанно и произвольно строить речевое высказывание в устной и письменной форме; рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности; установление причинно-следственных связей, построение логической цепи рассуждений,
— проводить анализ объектов с целью выделения признаков.
-умение формулировать собственное мнение и позицию,
— осознанное построение речевых высказываний,
-восприятие выступлений учащихся,
— участие в обсуждении содержания материала,
-планирование учебного сотрудничества с учителем и сверстниками,
-умение работать индивидуально и в группе, находить общее решение,
-умение формулировать, аргументировать и отстаивать свое мнение.
Добрый день уважаемые ученики, как ваше настроение? Готовы ли вы сегодня получить новые и интересные знания? Так давайте же приступим…
Прежде чем открыть для себя что то новое на уроке, я предлагаю вам сыграть в игру которая называется лото. (На столе карточки-лото). Я произношу пример, а вы должны вычеркнуть правильный ответ. (В конце разминки должно остаться два числа 81 и 74). Начнем.
9+12=21; 8+14=22; 13-7=6; 19-4=15; 7х9=63; 3х8=24; 21:7=3; 50:2=25; 59+17=76; 31-18=13;
15х3=45; 4х12=48; 99:11=9; 42:7=6
1 этап: Актуализация знаний.
Рассмотрите математическую запись: (фронтальная работа) выход к доске.
На решение примера дается 3 минуты, учащиеся решают после чего им задается вопрос. Можно ли назвать данное выражение уравнением? (да). А можно ли применить к этому выражению другое определение? (тождество)
Одно и то же равенство может рассматриваться как тождество и как уравнение.
Это зависит от условия к заданной работе: если требуется установить при каком значении переменной имеет место равенство, то это — уравнение.
Любое тождество должно быть………. (доказано).
Поэтому тема сегодняшнего урока ….(док-во тождеств), а целью будет научиться использовать способы доказательства тождеств.
2 этап. Изучение нового материала.
Скажите какие действия вы совершили при выполнении задания? А что такое тождественное преобразование выражений? (вопрос для дальнейшего изучения темы)
Задание по группам: Докажите тождество
На ваших столах карточки с примером, вы должны решить их самостоятельно и сформулировать способы решения данных выражений. На карточках есть подсказки чтобы правильно сформулировать эти способы. 5 минут на выполнение.
Карточки с заданием
Выпишите выражение в левой части указанного равенства, раскройте скобки и приведите подобные слагаемые, сравните полученное выражение с выражением правой части, сделайте вывод.
5х – 7 = 28х – 3 – х – 4 – 22х
Выпишите выражение правой части указанного равенства, приведите подобные слагаемые, сравните полученное выражение с выражением левой части и сделайте вывод.
(х – 5)(х + 2) = (х + 4)(х – 7) + 18
Выпишите сначала выражение левой части, раскрой те скобки и приведите подобные слагаемые, затем выпишите выражение правой части, раскройте скобки и приведите подобные слагаемые. Сравните полученные выражения, сделайте вывод.
Группы высказывают свое мнение.
Хорошо, а сейчас проверим себя. На экране появляются равенства. Найдите равенство которое не будет являться тождеством, и встаньте если равенство является тождеством, если же нет то оставайтесь на месте.
— Что же нам необходимо сделать, чтобы доказать, что равенство является тождеством? Предполагаемые ответы учащихся:
Выписать левую часть равенства, ее преобразовать и убедиться, что она равна правой.
или
Выписать правую часть равенства, ее преобразовать и убедиться, что она равна левой.
или
Преобразовать и левую и правую часть равенства и убедиться в том, что они равны одному и тому же выражению.
— А если не будет выполняться то, о чем мы только что сказали? Предполагаемый ответ учащихся: Равенство не будет являться тождеством.
Оцените свою деятельность:
На ваших столах лежат листочки с графиком.
Вам нужно построить график того как вы поняли тему урока. На оси ординат расположены баллы от 1 до 9, а на оси абсцисс этапы нашего урока. Соотнесите каждый этап урока с баллами.