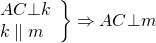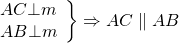Докажите что серединные перпендикуляры к сторонам треугольника пересекаются в одной точке

Свойство серединных перпендикуляров к сторонам треугольника

Три серединных перпендикуляра к сторонам треугольника пересекаются в одной точке, являющейся центром окружности, описанной вокруг треугольника

Пусть m – серединный перпендикуляр к стороне АВ, n – серединный перпендикуляр к стороне ВС, прямые m и n пересекаются в точке О.

Серединный перпендикуляр к отрезку – это множество точек, равноудаленных от его концов.

Получаем, что точка О равноудалена также от точек А и С, то есть – серединному перпендикуляру к АС.

Это значит, что три серединных перпендикуляра к сторонам треугольника пересекаются в одной точке. Точка О равноудалена от А, В и С и потому является центром окружности, описанной вокруг треугольника АВС.

Это полезно

В нашей статье вы найдете всю необходимую теорию для решения задания №9 ЕГЭ по теме «Графики функций». Это задание появилось в 2022 году в вариантах ЕГЭ Профильного уровня.

Источник

Серединные перпендикуляры к сторонам треугольника

Свойство серединных перпендикуляров к сторонам треугольника

Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.

Д ано:

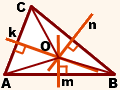
m, n, k — серединные перпендикуляры к сторонам AB, BC, AC

Доказать: m, n, k пересекаются в одной точке.

Сначала докажем, что серединные перпендикуляры к двум сторонам треугольника пересекаются в одной точке.

Предположим, что m и k не пересекаются. Тогда m ∥ k.

Но прямые AB и AC пересекаются в точке A. Пришли к противоречию. Следовательно, прямые m и k пересекаются.

Обозначим точку пересечения прямых m и k как O.

По свойству серединного перпендикуляра к отрезку AO=OC и AO=BO. Следовательно, и OC=BO. Значит, точка O равноудалена от концов отрезка BC, следовательно, лежит на серединном перпендикуляре n к этому отрезку. Таким образом, все три серединных перпендикуляра m, n, k к сторонам треугольника ABC пересекаются в одной точке O.

Что и требовалось доказать.

Точка пересечения серединных перпендикуляров к сторонам треугольника является центром описанной около этого треугольника окружности

Точка пересечения серединных перпендикуляров к сторонам треугольника — одна из четырех замечательных точек треугольника.

Источник

Докажите что серединные перпендикуляры к сторонам треугольника

Здравствуйте!
На зачете было задание «Докажите что серединные перпендикуляры к сторонам треугольника…». Дальше не помню. Кто знает что там дальше и как это доказать? Срочно нужно!
Спасибо!

Докажем, что серединные перпендикуляры к сторонам треугольника будут пересекаться в одной точке.
Данное свойство серединных перпендикуляров будем доказывать от противоположного.

Доказательство.
Рассмотрим произвольный треугольник NRP. Точкой M сторона NR делится пополам, а точкой S — сторона RP.
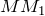
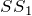
Проведем к его боковым сторонам NR и RP перпендикуляры и . Данные перпендикуляры пересекутся в точке О.
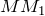
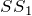
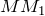
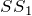
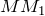
Предположим, что перпендикуляры и не пересекутся. Это значит, что они параллельны. В таком случае прямая RN, которая перпендикулярна прямой , будет перпендикулярной и к прямой , которая параллельна .
Это невозможно, так как тогда через точку R должны проходить две прямые RN и RP, которые перпендикулярны к прямой .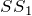
Так как любая точка серединного перпендикуляра, проведенного к стороне, равноудалена от его вершин, то ON=OR и OR=OP. Из этого следует, что ON=OP, что означает равноудаленность точки О от концов стороны NP. Таким образом, все три серединных перпендикуляра, проведенных к сторонам произвольного треугольника NRP, пересекаются в одной точке, что и требовалось доказать.
Доказательство завершено.

Источник