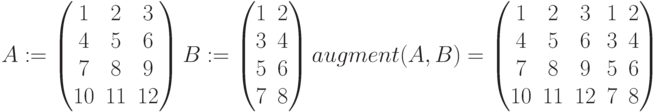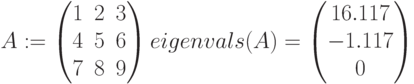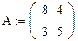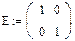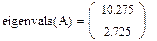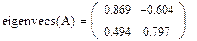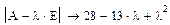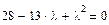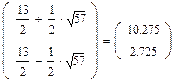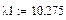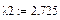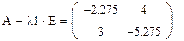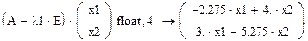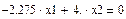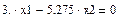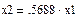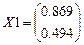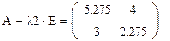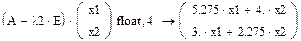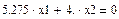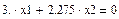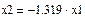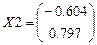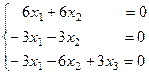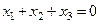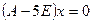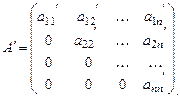Eigenvals в маткаде что это
Встроенные функции MathCAD
Часто используемые функции
ceil(y) – возвращает наименьшее целое, большее или равное y. Значение y должно быть вещественным числом:
cols(A) – число столбцов матрицы А.
csort(B,n) – сортирует строки матрицы В таким образом, чтобы расположить элементы столбца n в порядке возрастания. Нумерация столбцов по умолчанию начинается с нуля:
eigenvals(A) – определяет вектор собственных значений для квадратной матрицы А:
find(x,y,…) – возвращает значения x,y,…, удовлетворяющие ограничениям: равенствам или неравенствам, заданным в блоке given решения уравнений. Число уравнений должно равняться числу неизвестных.
floor(y) – возвращает наибольшее целое, меньшее или равное y. Значение y должно быть вещественным числом:
identity(n) – создает единичную матрицу размером
length(v) – длина вектора v.
max(v) – максимальный по значению элемент вектора v.
min(v) – минимальный по значению элемент вектора v.
mean(M) – среднее арифметическое элементов вектора или матрицы.
median(v) – медиана вектора. Элементы вектора должны быть заданы в порядке возрастания:
rbeta (m, s 1, s2)Возвращает вектор m случайных чисел, имеющих бэта-распределение. 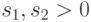
rgamma (m, s) Возвращает вектор m случайных чисел, имеющих гамма- распределение, 
rgeom (m, p) Возвращает вектор m случайных чисел, имеющих геометрическое распределение. 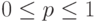
rlogis (m, l, s) Возвращает вектор m случайных чисел, имеющих логистическое распределение, в котором l является п а раметром расположения, а 
rpois (m,d) Возвращает вектор m случайных чисел, имеющих распределение Пуассона. 
rt (m, d) Возвращает вектор m случайных чисел, имеющих t-распределение Стьюдента. 
runif (m, a, b) Возвращает вектор m случайных чисел, имеющих равномерное распределение, в котором b и a являются граничными точками интервала. 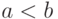
rnd (x) Возвращает равномерно распределенное случайное число между 0 и x. Эквивалент runif (1, 0, x).
round(y,n) – округляет вещественное число y до n знаков справа от десятичной точки. Если n отсутствует, то y округляется до ближайшего целого числа. Если n Нумерация строк по умолчанию начинается с нуля.
submatrix(M,ir,jr,ic,jc) – подматрица, состоящая из элементов матрицы М, содержащихся в строках от ir до jr и столбцах от ic до jc:
Встроенные функции MathCAD
Часто используемые функции
ceil(y) – возвращает наименьшее целое, большее или равное y. Значение y должно быть вещественным числом:
cols(A) – число столбцов матрицы А.
csort(B,n) – сортирует строки матрицы В таким образом, чтобы расположить элементы столбца n в порядке возрастания. Нумерация столбцов по умолчанию начинается с нуля:
eigenvals(A) – определяет вектор собственных значений для квадратной матрицы А:
find(x,y,…) – возвращает значения x,y,…, удовлетворяющие ограничениям: равенствам или неравенствам, заданным в блоке given решения уравнений. Число уравнений должно равняться числу неизвестных.
floor(y) – возвращает наибольшее целое, меньшее или равное y. Значение y должно быть вещественным числом:
identity(n) – создает единичную матрицу размером
length(v) – длина вектора v.
max(v) – максимальный по значению элемент вектора v.
min(v) – минимальный по значению элемент вектора v.
mean(M) – среднее арифметическое элементов вектора или матрицы.
median(v) – медиана вектора. Элементы вектора должны быть заданы в порядке возрастания:
rbeta (m, s 1, s2)Возвращает вектор m случайных чисел, имеющих бэта-распределение. 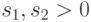
rgamma (m, s) Возвращает вектор m случайных чисел, имеющих гамма- распределение, 
rgeom (m, p) Возвращает вектор m случайных чисел, имеющих геометрическое распределение. 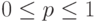
rlogis (m, l, s) Возвращает вектор m случайных чисел, имеющих логистическое распределение, в котором l является п а раметром расположения, а 
rpois (m,d) Возвращает вектор m случайных чисел, имеющих распределение Пуассона. 
rt (m, d) Возвращает вектор m случайных чисел, имеющих t-распределение Стьюдента. 
runif (m, a, b) Возвращает вектор m случайных чисел, имеющих равномерное распределение, в котором b и a являются граничными точками интервала. 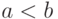
rnd (x) Возвращает равномерно распределенное случайное число между 0 и x. Эквивалент runif (1, 0, x).
round(y,n) – округляет вещественное число y до n знаков справа от десятичной точки. Если n отсутствует, то y округляется до ближайшего целого числа. Если n Нумерация строк по умолчанию начинается с нуля.
submatrix(M,ir,jr,ic,jc) – подматрица, состоящая из элементов матрицы М, содержащихся в строках от ir до jr и столбцах от ic до jc:
Eigenvals в маткаде что это
Mathcad содержит функции для обычных в линейной алгебре действий с массивами. Эти функции предназначены для использования с векторами и матрицами. Если явно не указано, что функция определена для векторного или матричного аргумента, не следует в ней использовать массивы как аргумент. Обратите внимание, что операторы, которые ожидают в качестве аргумента вектор, всегда ожидают вектор-столбец, а не вектор-строку. Чтобы заменить вектор-строку на вектор-столбец, используйте оператор транспонирования [Ctrl]1.
Если Вы используете Mathcad PLUS, Вы будете также иметь несколько дополнительных функций, определенных для векторов. Эти функции скорее предназначены для анализа данных, чем для действий с матрицами. Они обсуждены в Главе “Встроенные функции”.
Размеры и диапазон значений массива
В Mathcad есть несколько функций, которые возвращают информацию относительно размеров массива и диапазона его элементов. Рисунок 10 показывает, как эти функции используются.
| Имя функции | Возвращается. |
| rows(A) | Число строк в массиве A. Если А — скаляр, возвращается 0. |
| cols(A) | Число столбцов в массиве A. Если A скаляр, возвращается 0. |
| length(v) | Число элементов в векторе v. |
| last(v) | Индекс последнего элемента в векторе v. |
| max(A) | Самый большой элемент в массиве A. Если A имеет комплексные элементы, возвращает наибольшую вещественную часть плюс i, умноженную на наибольшую мнимую часть. |
| min(A) | Самый маленький элемент в массиве A. Если A имеет комплексные элементы, возвращает наименьшую вещественную часть плюс i, умноженную на наименьшую мнимую часть. |
Рисунок 10: Векторные и матричные функции для нахождения размера массива и получения информации относительно диапазона элементов.
Специальные типы матриц
Можно использовать следующие функции, чтобы произвести от массива или скаляра матрицу специального типа или формы. Функции rref, diag и geninv доступны только в Mathcad PLUS.
Рисунок 11: Функции для преобразования массивов. Обратите внимание, что функции diag и rref являются доступными только в Mathcad PLUS.
Специальные характеристики матрицы
Можно использовать функции из следующей таблицы, чтобы найти след, ранг, нормы и числа обусловленности матрицы. Кроме tr, все эти функции доступны только в Mathcad PLUS.
| Имя функции | Возвращается. |
| tr(M) | Сумма диагональных элементов, называемая следом M. |
| Е rank(A) | Ранг вещественной матрицы A. |
| Е norm1(M) | L1 норма матрицы M. |
| Е norm2(M) | L2 норма матрицы M. |
| Е norme(M) | Евклидова норма матрицы M. |
| Е normi(M) | Равномерная норма матрицы M. |
| Е cond1(M) | Число обусловленности матрицы M, основанное на L1 норме. |
| Е cond2(M) | Число обусловленности матрицы M, основанное на L2 норме. |
| Е conde(M) | Число обусловленности матрицы M, основанное на евклидовой норме. |
| Е condi (M) | Число обусловленности матрицы M, основанное на равномерной норме. |
Формирование новых матриц из существующих
В Mathcad есть две функции для объединения матриц вместе — бок о бок, или одна над другой. В Mathcad также есть функция для извлечения подматрицы. Рисунки 12 и 13 показывают некоторые примеры.
| Имя функции | Возвращается. |
| augment (A, B) | Массив, сформированный расположением A и B бок о бок. Массивы A и B должны иметь одинаковое число строк. |
| stack (A, B) | Массив, сформированный расположением A над B. Массивы A и B должны иметь одинаковое число столбцов. |
| submatrix (A, ir, jr, ic, jc) | Субматрица, состоящая из всех элементов, содержащихся в строках с ir по jc и столбцах с ic по jc. Чтобы поддерживать порядок строк и-или столбцов, удостоверьтесь, что ir |
Рисунок 12: Объединение матриц функциями stack и augment.
Рисунок 13: Извлечение субматрицы из матрицы при помощи функции submatrix.
Собственные значения и собственные векторы
В Mathcad существуют функции eigenval и eigenvec для нахождения собственных значений и собственных векторов матрицы. В Mathcad PLUS также есть функция eigenvecs для получения всех собственных векторов сразу. Если Вы используете Mathcad PLUS, Вы будете также иметь доступ к genvals и genvecs для нахождения обобщенных собственных значений и собственных векторов. Рисунок 14 показывает, как некоторые из этих функций используются.
Рисунок 14: Нахождение собственных значений и собственных векторов.
Рисунок 15: Использование eigenvecs для одновременного нахождения всех собственных векторов.
Если Вы используете Mathcad PLUS, Вы будете иметь доступ к некоторым дополнительным функциям для выполнения специальных разложений матрицы: QR, LU, Холесского, и по сингулярным базисам. Некоторые из этих функций возвращают две или три матрицы, соединенные вместе в одну большую матрицу. Используйте submatrix, чтобы извлечь эти две или три меньшие матрицы. Рисунок 16 показывает пример.
Рисунок 16: Использование функции submatrix для извлечения результата из функции rq. Используйте submatrix, чтобы извлечь подобным образом результаты из функций lu и svd. Обратите внимание, что эти функции доступны только в Mathcad PLUS.
Решение линейной системы уравнений
Если Вы используете Mathcad PLUS, Вы сможете использовать функцию lsolve для решения линейной системы уравнений. Рисунок 17 показывает пример. Обратите внимание, что M не может быть ни вырожденной, ни почти вырожденной для использования с lsolve. Матрица называется вырожденной, если её детерминант равен нулю. Матрица почти вырождена, если у неё большое число обусловленности. Можно использовать одну из функций, описанных на странице 204, чтобы найти число обусловленности матрицы.
Возвращается.
 x=v.
x=v.Если Вы не используете Mathcad PLUS, Вы всё-таки можете решать систему линейных уравнений, используя обращение матрицы, как показано в нижнем правом углу Рисунка 9.
Рисунок 17: Использование lsolve для решения системы из двух уравнений с двумя неизвестными.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
Встроенные функции MathCAD
Часто используемые функции
ceil(y) – возвращает наименьшее целое, большее или равное y. Значение y должно быть вещественным числом:
cols(A) – число столбцов матрицы А.
csort(B,n) – сортирует строки матрицы В таким образом, чтобы расположить элементы столбца n в порядке возрастания. Нумерация столбцов по умолчанию начинается с нуля:
eigenvals(A) – определяет вектор собственных значений для квадратной матрицы А:
find(x,y,…) – возвращает значения x,y,…, удовлетворяющие ограничениям: равенствам или неравенствам, заданным в блоке given решения уравнений. Число уравнений должно равняться числу неизвестных.
floor(y) – возвращает наибольшее целое, меньшее или равное y. Значение y должно быть вещественным числом:
identity(n) – создает единичную матрицу размером
length(v) – длина вектора v.
max(v) – максимальный по значению элемент вектора v.
min(v) – минимальный по значению элемент вектора v.
mean(M) – среднее арифметическое элементов вектора или матрицы.
median(v) – медиана вектора. Элементы вектора должны быть заданы в порядке возрастания:
rbeta (m, s 1, s2)Возвращает вектор m случайных чисел, имеющих бэта-распределение. 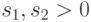
rgamma (m, s) Возвращает вектор m случайных чисел, имеющих гамма- распределение, 
rgeom (m, p) Возвращает вектор m случайных чисел, имеющих геометрическое распределение. 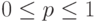
rlogis (m, l, s) Возвращает вектор m случайных чисел, имеющих логистическое распределение, в котором l является п а раметром расположения, а 
rpois (m,d) Возвращает вектор m случайных чисел, имеющих распределение Пуассона. 
rt (m, d) Возвращает вектор m случайных чисел, имеющих t-распределение Стьюдента. 
runif (m, a, b) Возвращает вектор m случайных чисел, имеющих равномерное распределение, в котором b и a являются граничными точками интервала. 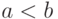
rnd (x) Возвращает равномерно распределенное случайное число между 0 и x. Эквивалент runif (1, 0, x).
round(y,n) – округляет вещественное число y до n знаков справа от десятичной точки. Если n отсутствует, то y округляется до ближайшего целого числа. Если n Нумерация строк по умолчанию начинается с нуля.
submatrix(M,ir,jr,ic,jc) – подматрица, состоящая из элементов матрицы М, содержащихся в строках от ir до jr и столбцах от ic до jc:
Встроенные функции MathCad для вычисления собственных векторов и собственных значений матриц



Для решения задач на собственные векторы и собственные значения в Mathcad встроено несколько функций, реализующих довольно сложные вычислительные алгоритмы:
— eigenvals(A) – вычисляет вектор, элементами которого являются собственные значения матрицы А;
— eigenvecs(A) – вычисляет матрицу, содержащую нормированные собственные векторы, соответствующие собственным значениям матрицы А.
Пример. Найти собственные значения и собственные векторы матрицы с помощью MathCad.
1. Задаем системную переменную и матрицы А (исходную) и Е (единичную):
2. Находим собственные значения и собственные векторы матрицы А с помощью встроенных функций MathCad:
3. Находим собственные значения и собственные векторы матрицы А вручную. Для этого составляем характеристический определитель и вычисляем характеристический полином:
4. Приравниваем его нулю нажатием Ctrl+= (получаем характеристическое уравнение):
5. Находим корни характеристического уравнения с помощью символьных вычислений (подсвечиваем λ нажатием мыши и выбираем в меню Символы®Переменные®Вычислить, затем нажимаем символ =)
Это и есть собственные значения матрицы А.
7. Далее найдем собственные векторы матрицы А вручную. Для этого запишем левую часть системы уравнений:
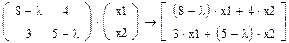
где x1, x2 – элементы собственных векторов, соответствующих собственным значениям λ.
8. Получим собственный вектор, соответствующий собственному значению λ1:
Запишем каждое уравнение системы отдельно (приравниваем их нулю нажатием Ctrl+=)
Из первого уравнения выразим х2 (подсвечиваем λ нажатием мыши и выбираем в меню Символы® Переменные® Вычислить)
Принимаем х1=0.869 (согласно пункту 2)
Собственный вектор, соответствующий собственному значению λ1:
9. Получим собственный вектор, соответствующий собственному значению λ2:
Запишем каждое уравнение системы отдельно (приравниваем их нулю нажатием Ctrl+=)
Из первого уравнения выразим х2 (подсвечиваем λ нажатием мыши и выбираем в меню Символы® Переменные® Вычислить)
Принимаем х1=-0.604 (согласно пункту 2)
Тогда х2= –1.319×(–0.604)=0.797
Собственный вектор, соответствующий собственному значению λ2:
Для собственных векторов матрицы справедливы следующие утверждения:
1. Собственные векторы матрицы, отвечающие различным собственным значениям, линейно независимы.
2. Если число различных корней матрицы n-го порядка равно n, то в пространстве 
3. Базис из собственных векторов матрицы А существует в том и только в том случае, когда сумма размерностей собственных подпространств равна n. Такая матрица называется матрицей простой структуры. Если 
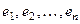
4. Матрица простой структуры подобна диагональной матрице, т.е. 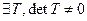
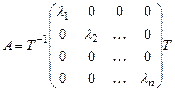
где 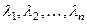

5. Все корни характеристического многочлена симметрической матрицы действительны, т.е.
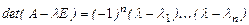
6. Собственные векторы симметрической матрицы, отвечающие различным собственным значениям, ортогональны.
7. Для симметрической матрицы 
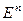
Решим еще два примера на нахождение собственных векторов и собственных значений матрицы.
Пример 1. Найти собственные векторы и собственные значения матрицы
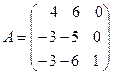
Решение. Находим корни характеристического многочлена
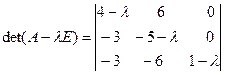
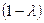
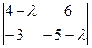
= 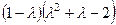
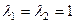
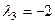
Ищем собственные векторы с собственным значением 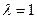
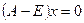
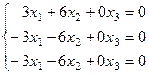
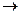
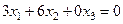
Общее решение системы 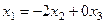
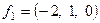
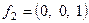
Собственный вектор для 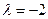
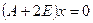
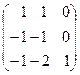
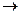
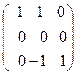
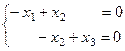
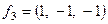
Ответ. 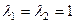
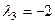
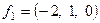
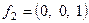
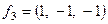
Пример 2. Найти ортонормированный базис из собственных векторов симметрической матрицы
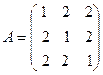
Находим характеристический многочлен матрицы 
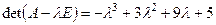
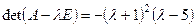
Найдем собственные векторы с собственным значением 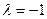
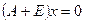
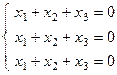
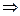
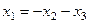
Базис в пространстве решений 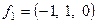
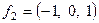
Так как мы ищем ортонормированный базис, то ортогонализуем систему 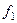
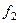
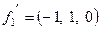
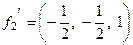
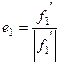
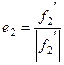
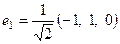
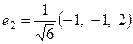
Нашли ортонормированный базис в собственном подпространстве с собственным значением 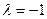
Найдем собственный вектор для собственного значения 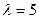
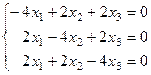
Решаем методом Гаусса, получим 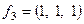
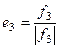
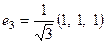
Ответ. Искомый ортонормированный базис 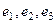
Преобразование подобия (8) можно использовать для упрощения исходной матрицы, а задачу вычисления её собственных значений свести к аналогичной задаче для более простой матрицы. Очевидно, самым лучшим упрощением исходной матрицы было бы приведение её к треугольному виду:
Тогда характеристическая матрица С так же имела бы треугольный вид. Как известно, определитель треугольной матрицы равен произведению ее диагональных элементов, поэтому характеристический многочлен в этом случае имеет вид:
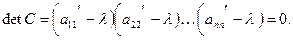
Собственные значения матрицы, равные корням этого многочлена, можно получить сразу.
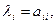
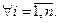
Таким образом, собственные значения треугольной матрицы равны её диагональным элементам.
Некоторые типы матриц удается привести к треугольному виду с помощью преобразований подобия. В частности, симметрическую матрицу можно привести к диагональному виду. На практике часто используется приведение симметрической матрицы к трехдиагональному виду.
Существует ряд методов, основанных на преобразовании подобия, позволяющие привести исходную матрицу к более простой структуре.