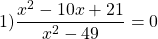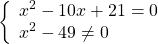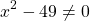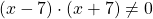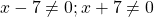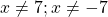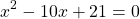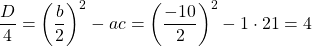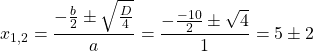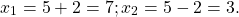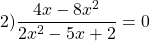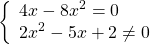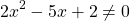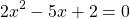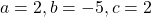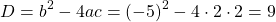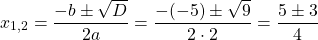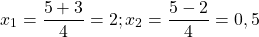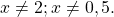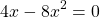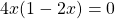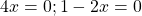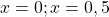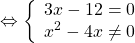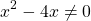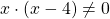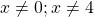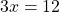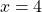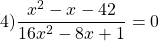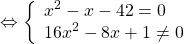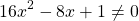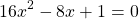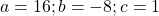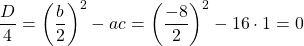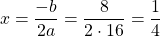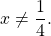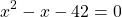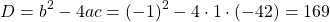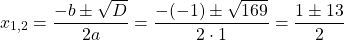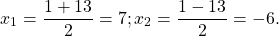Если в знаменателе 0 чему равна дробь
Десятичные дроби
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие десятичной дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Свойства десятичных дробей
Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
Обучение на курсах по математике — отличный способ закрепить полученные знания на практике и подтянуть сложные темы.
Как записать десятичную дробь
Давайте разберем на примерах, как записывается десятичная дробь. Небольшая напоминалка: сначала пишем целую часть, ставим запятую и после записываем числитель дробной части.
Пример 1. Перевести обыкновенную дробь 16/10 в десятичную.
Пример 2. Перевести 37/1000 в десятичную дробь.
Ответ: 37/1000 = 0,037.
Как читать десятичную дробь
Чтобы учитель вас правильно понял, важно читать десятичные дроби грамотно. Сначала произносим целую часть с добавлением слова «целых», а потом дробную с обозначением разряда — он зависит от количества цифр после запятой:
| Сколько цифр после запятой? | Читается, как |
|---|---|
| одна цифра — десятых; | 1,3 — одна целая, три десятых; |
| две цифры — сотых | 2,22 — две целых, двадцать две сотых; |
| три цифры — тысячных; | 23,885 — двадцать три целых, восемьсот восемьдесят пять тысячных; |
| четыре цифры — десятитысячных; | 0,5712 — ноль целых пять тысяч семьсот двенадцать десятитысячных; |
| и т.д. |
Сохраняй наглядную картинку, чтобы быстрее запомнить.
Преобразование десятичных дробей
Чтобы ни одна задача не смутила вас своей формулировкой, важно знать, как преобразовывать десятичные дроби в другие виды. Сейчас научимся!
Как перевести десятичную дробь в проценты
Уже в пятом классе задачки по математике намекают, что дроби как-то связаны с процентами. И это правда: процент — это одна сотая часть от любого числа, обозначают его значком %.
Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить наше число на 100, как в примере выше.
А чтобы перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Давайте на примере:
Выразить дробь в процентах просто: сначала превратим её в десятичную дробь, а потом применим предыдущее правило.
2/5 = 0,4
0,4 · 100% = 40%
8/25 = 0,32
0,32 · 100% = 32%
Чтобы разрезать торт на равные кусочки и не обижать гостей, нужно всего-то запомнить соотношения частей и целого. Наглядная табличка — наш друг-помощник:
Преобразование десятичных дробей
Десятичная дробь — это число с остатком, где остаток стоит после целой части и разделяется запятой.
Смешанная дробь — это тоже число с остатком, но остаток записывают в виде простой дроби (с черточкой).
Чтобы переводить десятичные дроби в смешанные, не нужно запоминать особые алгоритмы. Достаточно понимать определения и правильно читать заданную дробь — этим школьники и занимаются в 5 классе. А теперь давайте потренируемся!
Пример 1. Перевести 5,4 в смешанное число.
Пример 2. Перевести 4,005 в смешанное число.
Ответ: 4,005 = 4 1/200.
Пример 3. Перевести 5,60 в смешанное число.
Как перевести десятичную дробь в обыкновенную
Не будем придумывать велосипед и рассмотрим самый простой способ превращения десятичной дроби в обыкновенную. Вот, как это сделать:
Не забывайте про минус в ответе, если пример был про отрицательное число. Очень обидная ошибка!
Действия с десятичными дробями
С десятичными дробями можно производить те же действия, что и с любыми другими числами. Рассмотрим самые распространенные на простых примерах.
Как разделить десятичную дробь на натуральное число
Пример 2. Разделить 183,06 на 45.
Ответ: 183,06 : 45 = 4,068.
Как разделить десятичную дробь на обыкновенную
Чтобы разделить десятичную дробь на обыкновенную или смешанную, нужно представить десятичную дробь в виде обыкновенной, а смешанное число записать, как неправильную дробь.
Пример 1. Разделить 0,25 на 3/4.
Пример 2. Разделить 2,55 на 1 1/3.
Ответ: 2,55 : 1 1/3 = 1 73/80.
Как умножить десятичную дробь на обыкновенную
Чтобы умножить десятичную дробь на обыкновенную или смешанную, используют два правила за 6 класс. При первом приводим десятичную дробь к виду обыкновенной и потом умножаем на нужное число. Во втором случае приводим обыкновенную или смешанную дробь в десятичную и потом умножаем.
Пример 1. Умножить 2/5 на 0,8.
Пример 2. Умножить 0,28 на 6 1/4.
Ответ: 0,28 ∗ 6 1/4 = 0,8.
Дробь равна нулю
Когда дробь равна нулю?
Дробная черта — это знак деления. При делении нуля на любое число, кроме нуля, получим нуль. На нуль делить нельзя.
Таким образом, дробь равна нулю, если числитель равен нулю, а знаменатель отличен от нуля.
Решение многих задач в алгебре сводится к решению дробно рациональных уравнений, которые, в свою очередь, сводятся к уравнению типа «дробь равна нулю».
Схематически решение уравнения типа «дробь равна нулю» можно изобразить так:
Таким образом, чтобы решить уравнение типа «дробь равна нулю», надо:
1) Найти значения переменной, при которых знаменатель обращается в нуль.
2) Приравнять к нулю числитель и решить получившееся уравнение.
3) Проверить, нет ли среди корней уравнения «числитель равен нулю» значений, при которых знаменатель обращается в нуль. Если есть, их следует исключить.
Дробь равна нулю, если числитель равен нулю, а знаменатель — отличен от нуля, поэтому это уравнение равносильно системе
Находим значения переменной, при которых знаменатель обращается в нуль:
Можно приравнять выражение, стоящее в левой части неравенства, к нулю, и решать как обычное неполное квадратное уравнение. Можно решать как уравнение, только вместо знака равенства каждый раз писать «≠».
При этих значениях переменной выражение, стоящее в левой части уравнения, не имеет смысла (так как на нуль делить нельзя).
Решаем уравнение, в котором числитель равен нулю.
Так как D/4>0, уравнение имеет два корня:
Первый из корней — посторонний (он не удовлетворяет условию x≠7), поэтому в ответ записывает только корень 3. Ответ: 3.
Это уравнение равносильно системе
Его корни — значения переменной, при котором выражение, стоящее в левой части уравнения, не имеет смысла.
Общий множитель 4x выносим за скобки
Второй корень не подходит (он не удовлетворяет условию x≠0,5).
Переходим к решению уравнения 3x-12=0. Это — линейное уравнение. Неизвестное — в одну сторону, известное — в другую с противоположным знаком:
Полученный корень является посторонним, так как не удовлетворяет условию x≠4. Значит, исходное уравнение типа «дробь равна 0» корней не имеет.
Решаем квадратное уравнение
Так как D/4=0, квадратное уравнение имеет один корень
Теперь решаем уравнение
Посторонних корней нет (оба корня удовлетворяют условию x≠1/4).
Обыкновенные дроби
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Доля целого
Доля — это каждая равная часть, из суммы которых состоит целый предмет.
Для примера возьмем два мандарина. Когда мы их почистим, то получим в каждом мандарине разное количество долек или долей. В одном может быть 6, а в другом — целых 9. Размеры долей у каждого мандарина тоже разные.
У каждой доли есть свое название: оно зависит от количества долей в конкретном предмете. Если в мандарите шесть долей — каждая из них будет определяться, как одна шестая от целого.
Понятие доли можно применить не только к предметам, но и величинам. Так, например, картина занимает четверть стены — при этом ее ширина треть метра.
Чтобы быстрее запомнить соотношения частей и целого, можно использовать наглядную табличку:
Понятие дроби
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которой можно представить число. Есть два формата записи:
Виды дробей:
Какие еще бывают дроби:
Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.
Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3\5.
Выделение целой части из неправильной дроби — это запись неправильной дроби в виде суммы натурального числа и правильной дроби. Например, 11/5 = 2 + 1/5.
Как устроена обыкновенная дробь
Обыкновенная дробь — это запись вида m/n, где m и n любые натуральные числа.
Такие дроби записываются с помощью двух натуральных чисел и горизонтальной черты, которая называется чертой дроби. Иногда ставится не горизонтальная черта, а косая.
Числитель обыкновенной дроби m/n — это натуральное число m, которое стоит над чертой. Числитель это делимое — то, что мы делим.
Знаменатель обыкновенной дроби m/n — натуральное число n, которое стоит под чертой. Знаменатель это делитель — то, на сколько делим.
Черта между числителем и знаменателем — символ деления.
Равные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых справедливо равенство: a * d = b * c. Пример равных дробей: 1/2 и 2/4, так как 1 * 4 = 2 * 2.
Неравные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых равенство: a * d = b * c не является верным.
Как устроена десятичная дробь
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. Выходит, что десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Свойства дробей
Основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же отличное от нуля число, то получится дробь, равная данной. Формула выглядит так:

Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
У нас есть отличные курсы по математике для учеников с 1 по 11 классы, записывайтесь!
Действия с дробями
С дробями можно выполнять те же действия, что и с обычными числами: складывать, вычитать, умножать и делить. А еще дроби можно сокращать и сравнивать между собой. Давайте попробуем.
Сравнение дробей
Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше.
Сравним 1/5 и 4/5. Как рассуждаем:
Чтобы сравнить дроби с разными знаменателями, нужно привести дроби к общему знаменателю. А после приведения дробей к общему знаменателю, можно применить правило сравнения дробей с одинаковыми знаменателями.
Пример. Сравнить 2/7 и 1/14.
Важно запомнить: любая неправильная дробь больше любой правильной. Потому что неправильная дробь всегда больше или равна 1, а правильная дробь всегда меньше 1.
Чтобы сравнить дроби с разными числителями и знаменателями, нужно:
Чтобы привести дроби к наименьшему общему знаменателю, нужно:
Сокращение дробей
Сокращение дроби — это деление числителя и знаменателя дроби на одно и то же натуральное число. Сократить дробь значит сделать ее короче и проще для восприятия. Например, дробь 1/3 выглядит намного проще и красивее, чем 27/81.
Сокращение дроби выглядит так: зачеркивают числитель и знаменатель, а рядом записывают результаты деления числителя и знаменателя на одно и то же число.
В этом примере делим обе части дроби на двойку.
Можно никуда не спешить и сокращать дроби последовательно, в несколько действий.
Сложение и вычитание дробей
При сложении и вычитании дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой вычитают числитель второй) и оставляют тот же знаменатель.
Не забудьте проверить, можно ли сократить дробь и выделить целую часть.
При сложении и вычитании дробей с разными знаменателями нужно найти наименьший общий знаменатель, сложить или вычесть полученные дроби (используем предыдущее правило).
Для этого запишем в столбик числа, которые в сумме дают значения делителей. Далее перемножаем полученное и получаем НОК.
НОК (15, 18) = 3 * 2 * 3 * 5 = 90
Полученные числа запишем справа сверху над числителем.
Ход решения одной строкой:
Сложение или вычитание смешанных чисел можно привести к отдельному сложению их целых частей и дробных частей. Для этого нужно действовать поэтапно:
Необходимо приводить к общему, если знаменатели разные. Для этого воспользуемся знаниями из предыдущего примера.
Если при сложении дробных частей получилась неправильная дробь, нужно выделить ее целую часть и прибавить к полученной ранее целой части.
Умножение и деление дробей
Произведение двух дробей равно дроби, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей:
Не забываем про сокращение. Это может облегчить вычисления.
Чтобы умножить два смешанных числа, надо:
Чтобы разделить дробь на дробь нужно выполнить следующую последовательность действий:
Другими словами это правило звучит так: чтобы разделить одну дробь на другую, надо первую умножить на обратную от второй.
Числа, произведение которых равно 1, называют взаимно обратными.
Как делить дроби с разными знаменателями? На самом деле одинаковые или разные знаменатели у дробей — неважно, потому что все дроби делятся по правилу, описанному выше.
Для деления смешанных чисел необходимо:
Деление дробей: теория и практика
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие дроби
Дробь — одна из форм представления числа в математике. Это запись, в которой a и b являются числами или выражениями. Существует два формата записи:
Над чертой принято писать делимое, которое является числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление. В 5 классе ребята это уже знают.
Дроби бывают двух видов:
Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 3/7 и 31/45.
Неправильной — ту, у которой числитель больше знаменателя или равен ему. Например, 21/4. Такое число является смешанным и читается, как пять целых одна четвертая, а записывается — 5 1\4.
Основные свойства дроби
1. Дробь не имеет значения, при условии, если делитель равен нулю.
2. Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.
3. Две дроби a/b и c/d называются равными, если a * d = b * c.
4. Если числитель и знаменатель умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Деление дробных чисел
Деление — арифметическое действие, по которому можно узнать, сколько раз одно число содержится в другом. А еще деление — это обратное действие умножения.
Свойства деления:
1. При делении на единицу получится такое же число:
2. На ноль делить нельзя.
3. Когда делим ноль на любое число, всегда получаем ноль:
4. Когда делим любое число на само себя получаем единичку:
5. Когда делим сумму на какое-либо число, можно разделить на него каждое слагаемое, а потом сложить полученное:
6. Когда делим разность на какое-нибудь число, можно разделить на него уменьшаемое и вычитаемое отдельно и из первого частного вычесть второе:
7. Когда делим произведение двух множителей на число, можно разделить на него любой из множителей и частное умножить на второй множитель:
Записывайся на онлайн обучение по математике, с лучшими учителями! Для учеников с 1 по 11 классы!
Деление обыкновенных дробей
Как делить дробь на дробь? Выполняем следующую последовательность действий:
Другими словами это правило звучит так: чтобы разделить одну дробь на другую, надо первую умножить на обратную от второй.
Как делить дроби с разными знаменателями? Тут все просто: пользуемся правилами выше, поскольку на практике нам неважно, одинаковые знаменатели или нет.
Деление дроби на натуральное число
Для деления дроби на натуральное число нужно:
Деление натурального числа на дробь
Чтобы поделить натуральное число на обыкновенную дробь нужно:
Деление на смешанное число
Для деления смешанных чисел необходимо:
Если урок в самом разгаре и посчитать нужно быстро — можно воспользоваться онлайн-калькулятором. Вот несколько подходящих: